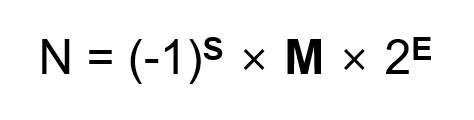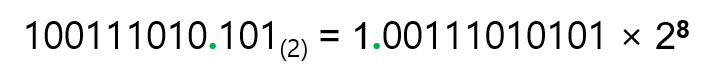숫자를 부동소수점 방식으로 표현하기¶
■ Table of Contents
숫자를 표현하는 다양한 방식¶
일상 생활에서 우리는 주로 10진수로 숫자를 표현합니다.
예를 들어 사과가 3개 있다고 표현하거나 온도가 13.5도라고 표현합니다.
이 숫자들을 2진수로 표현하면 정수 3은 2진수로 11 (2) 이 되고, 실수 13.5는 2진수로 1101.1 (2) 가 됩니다.
(10진수 0.1 (10) 은 1/10이고, 2진수 0.1 (2) 은 1/2입니다.)
컴퓨터는 숫자 0과 1을 이용해서 숫자를 표현하는데, 부동소수점 (floating point) 방식은 숫자를 0과 1을 이용해서 (근사해서) 표현하는 방식 중 하나입니다.
부동소수점에서 부동은 움직이지 않는다는 뜻의 不動이 아니라, 오히려 그 반대의 의미로 소수점이 떠다니며 움직인다는 의미의 부동 (浮動)입니다.
이 페이지에서는 IEEE 754 표준 방식으로 숫자를 부동소수점으로 표현하는 방법에 대해 소개합니다.
(IEEE 754는 전기 전자 기술자 협회 (IEEE)에서 개발한 표준 부동소수점 방식이며 현재 컴퓨터에서 가장 널리 쓰이는 방식입니다.)

IEEE Standard for Floating Point Arithmetic (IEEE 754).¶
부호, 지수, 가수¶
IEEE 754 부동소수점 표현에서 숫자는 아래와 같이 부호부, 지수부, 가수부의 세 부분으로 구성됩니다.
각 부분의 역할과 사용하는 비트 수는 아래와 같습니다.
부호부 (Sign) : 1비트. 숫자의 부호를 나타내며, 양수일 때 0, 음수일 때1이 됩니다.
지수부 (Exponent) :8비트. 지수를 나타냅니다.
가수부 (Mantissa) : 23비트. 가수 또는 유효숫자를 나타냅니다.

32비트 단정도 (single precision) 부동소수점 표현.¶
위의 그림과 같이 숫자를 표현하고 저장하기 위해 32비트 (4바이트)를 사용하는 방식을 단정도 (single precision)라고 합니다.
배정도 (double precision) 표현에서는 64비트 (8바이트)를 사용합니다.
부동소수점 변환 예시¶
숫자 -314.625를 IEEE 754 부동소수점 방식으로 표현해 보겠습니다.
가수부¶
두번째로 숫자의 절대값을 2진수로 표현합니다.
314.625는 2진수 100111010.101 (2) 가 됩니다.
이 2진수의 소수점을 아래와 같이 왼쪽으로 이동시켜서 소수점 왼쪽에 1만 남도록 합니다.
이제 2진수 100111010.101 (2) 를 아래와 같이 표현할 수 있는데, 이 방식을 정규화된 표현 방식이라고 합니다.
그리고 소수점의 오른쪽 부분 00111010101을 가수부 23비트의 앞에서부터 채워줍니다.
남는 자리는 0으로 채워줍니다.
지수부¶
이제 지수부를 채울 차례입니다.
지수는 8입니다.
지수 8에 bias인 127을 더해줍니다. (bias는 2 k-1 로 주어지는데 k는 지수부의 비트수 8입니다.)
아래와 같이 8에 bias를 더한 135를 2진수로 변환합니다.
변환한 2진수 10000111 (2) 을 8비트 지수부에 채워줍니다.
위와 같은 과정을 통해 숫자 -314.625를 32비트 단정도 부동소수점 방식으로 표현하면 11000011100111010101000000000000가 됩니다.
이 링크와 같은 웹사이트에서 간편하게 숫자를 부동소수점으로 변환해 볼 수 있습니다.