강화학습으로 순회 외판원 문제 풀기 (Traveling Salesman Problem)¶
순회 외판원 문제¶
외판원 문제 또는 순회 외판원 문제는 조합 최적화 문제의 일종이며 영어로는 Traveling Salesman Problem (TSP)라고 합니다.
예를 들어, 여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 시간 또는 거리로 주어졌을 때, 모든 도시들을 한 번씩 방문하고 시작점으로 돌아오는 최소 비용의 이동 순서를 구하는 문제입니다.
서울을 출발해서 대전, 부산, 제주를 한 번씩 거쳐서 가장 빨리 서울로 돌아오기 위한 이동 순서는 어떻게 결정할 수 있을까요?
방문할 도시의 수가 3개인 경우라면 고려해야 할 모든 경우의 수가 3×2×1 (3!)로 주어지므로 어려운 문제가 아니지만 방문 도시가 10개로 늘어난다면 그 경우의 수가 10! = 3628800가 되어 다루기 어려운 문제가 됩니다.
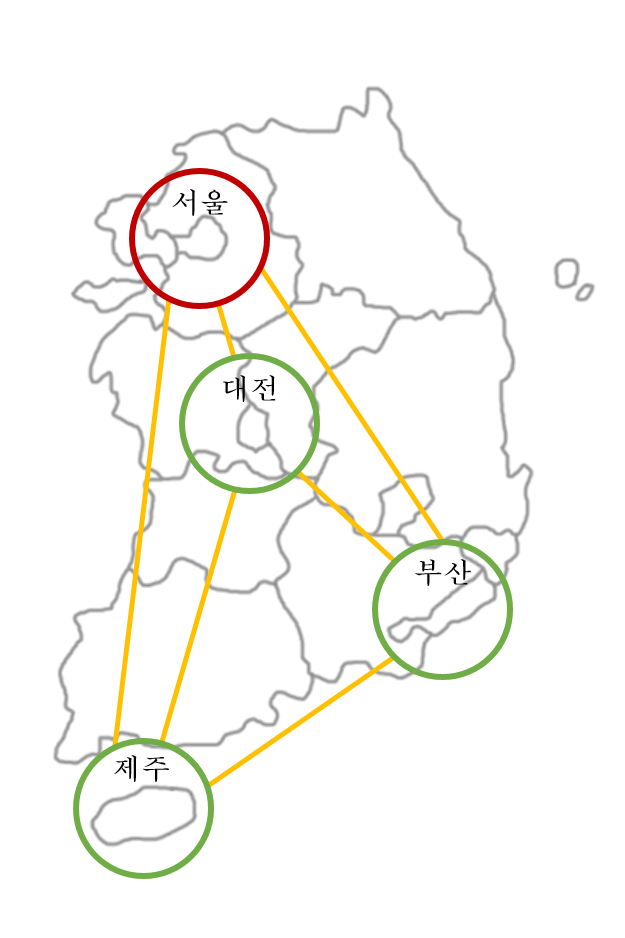
각 도시를 한 번씩 방문하고 시작점으로 돌아오기.¶
이 페이지에서는 강화학습의 알고리즘을 이용해서 순회 외판원 문제를 해결하는 방법에 대해 소개합니다.
Q-Learning¶
Q-Learning은 강화학습 (reinforcement learning)의 대표적인 학습 방식입니다.
강화학습은 에이전트 (agent)가 주어진 환경 (environment)의 어떤 상태 (state)에서 선택할 수 있는 여러가지 행동 (action) 중 하나를 취하고 환경으로부터 보상 (reward)를 받는 상황에서 적용할 수 있는 학습 기법입니다.
예를 들면, 아래와 같은 바둑 게임에서 에이전트는 바둑을 두는 사람, 환경은 바둑 게임의 환경 (규칙과 규격), 상태는 현재 바둑판의 상태, 행동은 바둑알을 놓을 위치가 됩니다. 또한 보상은 게임의 승패에 따라 결정됩니다. 즉, 어떤 상태에서 취하는 행동을 통해 보상을 받는 과정을 반복하면서 이 보상을 최대화하는 방향으로 학습이 이루어지게 됩니다.
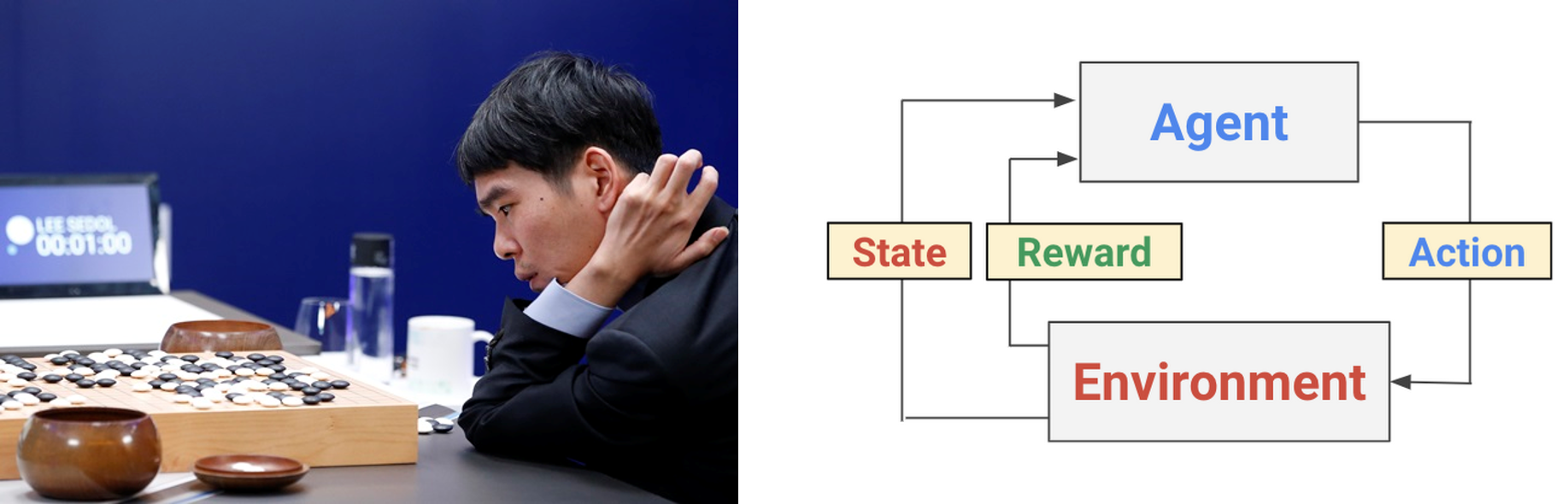
바둑 게임 (좌)과 강화학습 (우)의 과정.¶
Q-Learning에서 사용하는 중요한 학습 규칙 (learning rule)은 아래와 같습니다.
여기서 \(Q(s, a)\)는 Q-Value로서 현재 상태 s에서 행동 a를 취했을 때, 목적지에 도달하기까지 받는 할인된 보상의 총합의 기대치입니다.
\(\hat{Q} (s, a)\)는 \(Q(s, a)\)의 추정치이고, \(s'\)와 \(a'\)는 다음 상태와 다음 상태에서 취할 수 있는 행동입니다.
\(r(s, a)\)는 상태 \(s\)에서 행동 \(a\)를 취했을 때의 보상, 그리고 \(\gamma\)는 할인율 (discount factor)입니다.
문제 정의하기¶
앞에서 소개한 순회 외판원 문제를 아래와 같이 간단한 그림으로 표현할 수 있습니다.
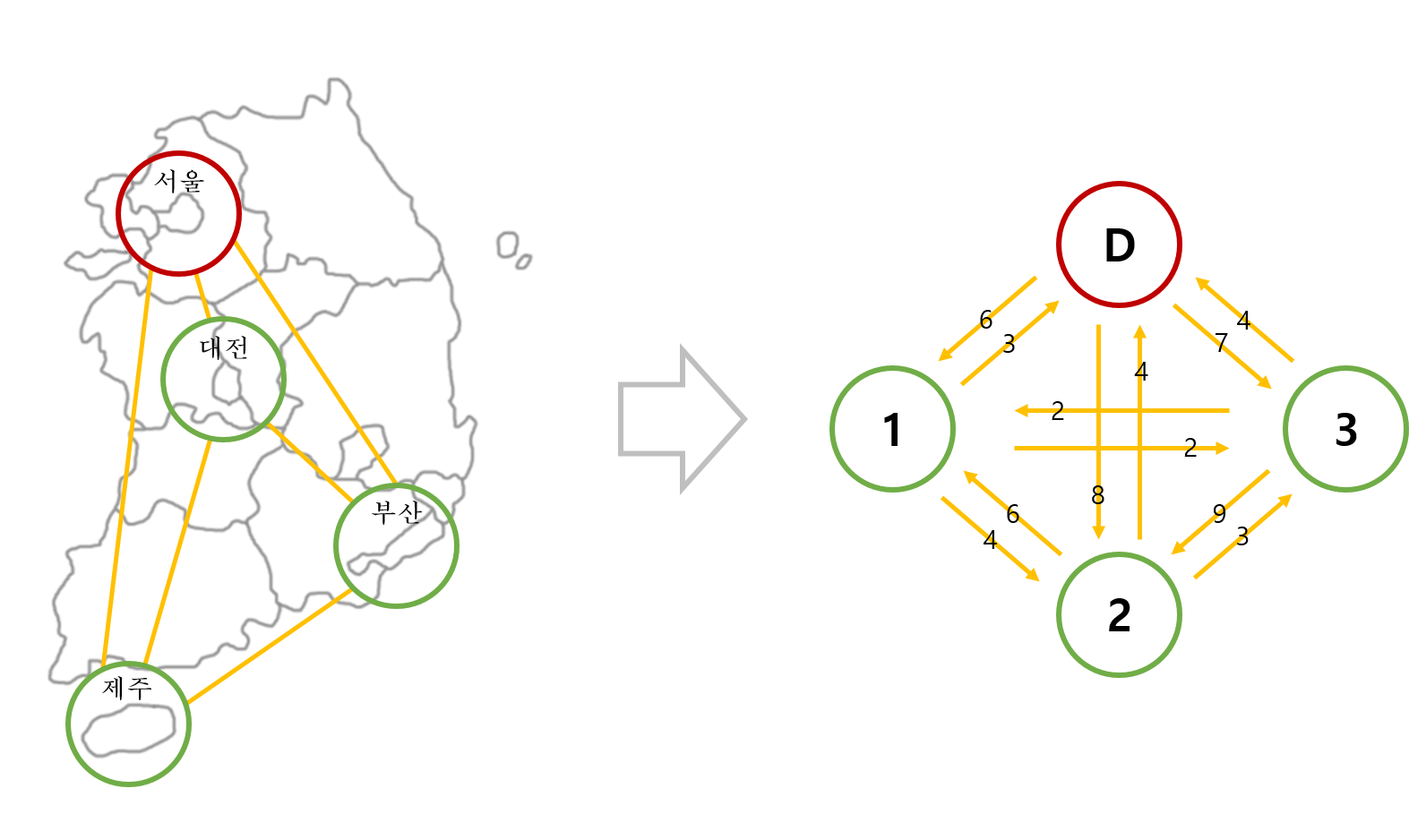
순회 외판원 문제를 간단하게 정의하기.¶
D는 출발지이고 1, 2, 3은 방문할 도시를 나타냅니다.
그리고 화살표 위의 숫자는 각 도시 간 이동 시간을 나타냅니다. 문제의 상황에 따라 이동 거리를 고려할 수도 있습니다.
이 문제의 상황을 Q-Learning의 요소에 대응시키면 아래와 같습니다.
상태 (State) : 지금까지 방문한 도시 + 현재 위치.
행동 (Action) : 다음 방문할 도시.
보상 (Reward) : 도시 간 이동 시간.
예를 들어, 도시 D에서 출발해서 도시 1의 위치로 이동한 상황이라고 할 때,
현재 상태는 {D, 1}, 이 상태에서 앞으로 취할 수 있는 행동은 {2, 3}, 각 행동에 대한 보상은 각각 4, 2가 됩니다.
Q-Table을 이용한 학습¶
Q-Learning은 Q-Value를 반복적으로 계산 및 갱신함으로써 이루어지는데 아래와 같은 Q-Table에 순서대로 Q-Value를 입력할 수 있습니다.
Q-Value의 초기값은 충분히 큰 값인 100으로 하고, 할인율 \(\gamma\)는 0.9로 설정하였습니다.
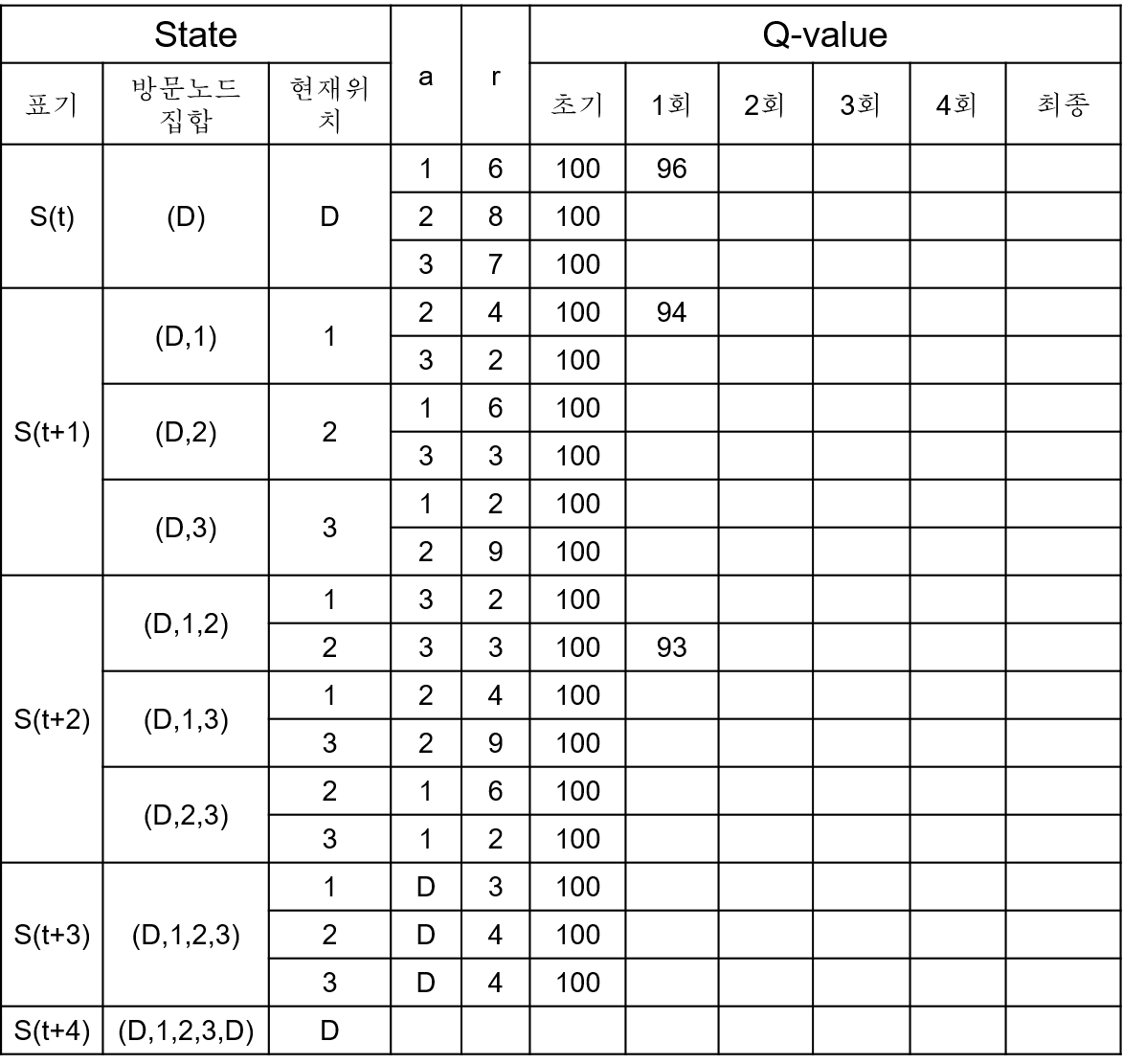
Q-Table을 이용한 학습 1.¶
출발 도시 D에서 1로 이동하는 선택에 대한 Q-Value는 아래와 같이 계산됩니다.
마찬가지로 도시 1에서 2로 이동하는 선택에 대한 Q-Value는 아래와 같이 계산됩니다.
도시 2에서 3으로 이동하는 선택에 대한 Q-Value는 아래와 같이 계산됩니다.
여러번의 반복적인 계산을 통해서 결과적으로 아래와 같은 Q-Table이 완성될 것을 알 수 있습니다.

Q-Table을 이용한 학습 2.¶
이제 모든 상태에서 모든 선택에 대한 Q-Value를 모두 얻었습니다.
처음 상태 D에서 도시 2로 이동하기 위한 Q-Value인 14.51은 어떤 의미를 가질까요?
이 Q-Value는 아래와 같이 계산되는 할인된 보상의 총합의 기대치입니다.
에이전트가 특정 상태에서 어떤 행동을 취하는 방식을 정책 (policy)이라고 합니다.
위의 Q-Table에서 최종적으로 얻은 Q-Value들을 참고해서 판단을 이어나가는 것은 최적화된 정책 (optimal policy)을 따르는 것입니다.
현재 상태가 D라면 가장 작은 Q-Value를 갖는 선택, 즉 도시 2로 이동하는 것이 앞으로 가장 적은 총 이동 시간을 기대할 수 있습니다.
결과적으로, D > 2 > 3 > 1 > D의 순서대로 이동하는 것이 가장 적은 이동 시간이 걸릴 것이라고 예상할 수 있습니다.
실제로 D > 2 > 3 > 1 > D 의순서로 움직였을 때 16시간으로 가장 적은 시간으로 이동할 수 있습니다.
하지만 Q-Table을 일일이 작성하는 작업은 방문할 도시가 많아질 경우 Q-Table의 크기가 매우 커진다는 문제점을 가집니다.
이제 Q-Network를 이용한 학습 기법에 대해 소개합니다.
Q-Network¶
Q-Learning을 위해 아래 그림과 같은 간단한 뉴럴 네트워크 (인공 신경망)를 이용하는데 이를 Q-Network라고 합니다.
입력층 (input layer), 은닉층 (hidden layer), 출력층 (output layer)을 각각 하나씩 사용해서 구성하고,
은닉층의 활성화 함수 (activation function)는 ReLU (Rectified Linear Unit)를 사용했습니다.
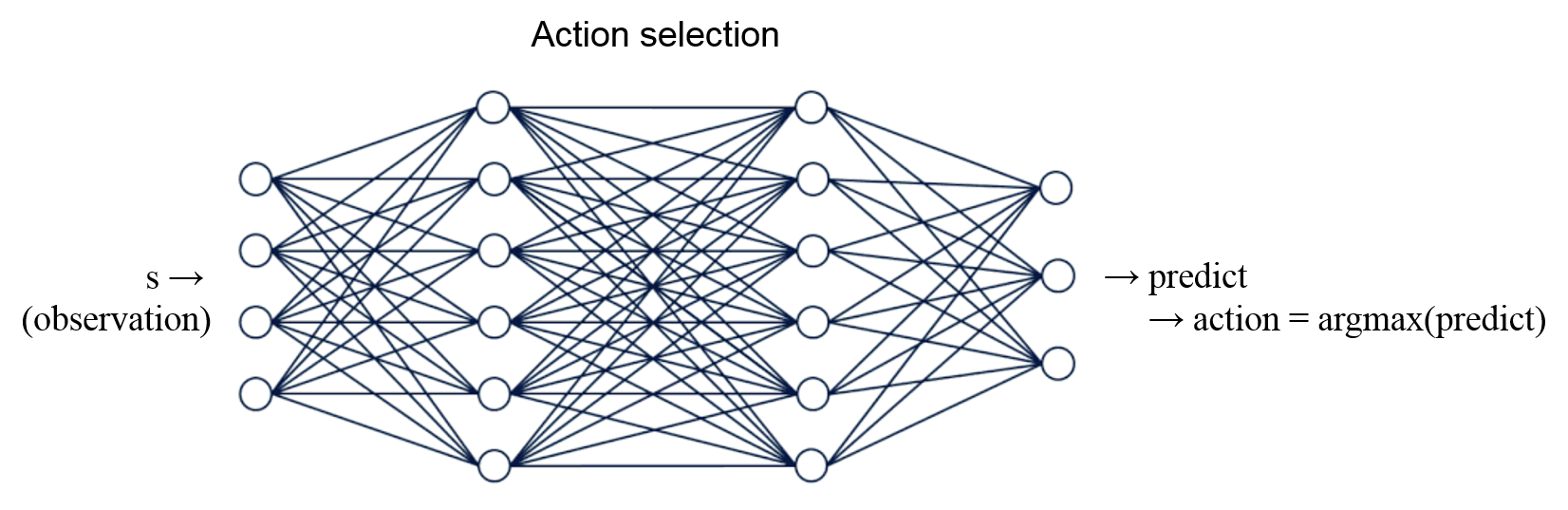
Q-Learning을 위한 뉴럴 네트워크 (인공 신경망).¶
모델 생성과 시각화하기¶
우선 신경망 모델을 하나 만들고, 시각화해서 이미지로 저장해 보겠습니다.
import numpy as np
import random as rd
import tensorflow as tf
from tensorflow.keras.utils import plot_model
def rargmin(vector):
m = np.amin(vector)
indices = np.nonzero(vector == m)[0]
return rd.choice(indices)
# Create a neural network model
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(128, input_shape=(8,), activation=tf.nn.relu),
tf.keras.layers.Dense(4, activation='linear')
])
# Create and Set weight values
weight0 = np.random.rand(8, 128) * 1.0
weight1 = np.zeros(128)
weight2 = np.random.rand(128, 4) * 0.5
weight3 = np.zeros(4)
weights = np.array([weight0, weight1, weight2, weight3])
model.set_weights(weights)
# Visualize
plot_model(model, to_file='model_shapes.png', show_shapes=True)
결과는 아래와 같습니다.
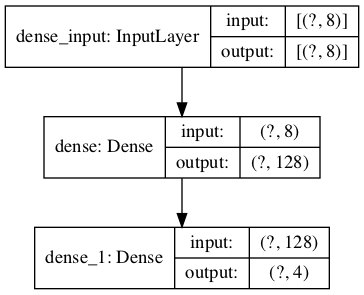
뉴럴 네트워크 모델 시각화.¶
학습하기¶
아래 코드는 위에서 만든 신경망 모델, 즉 Q-Network를 이용해서 Q-Table에서 얻었던 Q-Value의 근사치를 얻는 예제입니다.
Q-Network의 8개의 입력은 현재 몇 번째 방문한 도시인지, 그리고 도시의 번호를 One-hot encoding으로 나타낸 것입니다.
4개의 출력은 현재 상태에서 각 선택에 대한 Q-Value를 출력합니다.
import numpy as np
import random as rd
import tensorflow as tf
from tensorflow.keras.utils import plot_model
def rargmin(vector):
m = np.amin(vector)
indices = np.nonzero(vector == m)[0]
return rd.choice(indices)
# Create a neural network model
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(128, input_shape=(8,), activation=tf.nn.relu),
tf.keras.layers.Dense(4, activation='linear')
])
# Create and Set weight values
weight0 = np.random.rand(8, 128) * 1.0
weight1 = np.zeros(128)
weight2 = np.random.rand(128, 4) * 0.5
weight3 = np.zeros(4)
weights = np.array([weight0, weight1, weight2, weight3])
model.set_weights(weights)
# Visualize
# plot_model(model, to_file='model_shapes.png', show_shapes=True)
# Compile
model.compile(optimizer='adam',
loss='mean_squared_error',
learning_rate=0.001)
num_episodes = 2000
time = np.array([[10, 6, 8, 7],
[3, 10, 4, 2],
[4, 6, 10, 3],
[4, 2, 9, 10]])
for i in range(num_episodes):
done = False
total_reward = 0 # Total reward
state = 0 # Initial state
seq = [state]
togo = [1, 2, 3]
# epsilon
e = 0.85 if i < 0.98 * num_episodes else 0.01
# e = 1 / ((i / 50) + 10)
while not done:
seq_in = np.identity(4)[len(seq) - 1] # Initial: [1 0 0 0] > [0 0 0 1]
state_in = np.identity(4)[state]
input = np.concatenate((seq_in, state_in)) # Concatenate
input = input.reshape((1, 8)) # Reshape to NN input
output = model.predict(input)
# Select an action
if np.random.rand() < e:
action = np.random.randint(0, 4)
else:
action = rargmin(output[0])
if action in togo:
seq.append(action)
togo.remove(action)
reward = time[state][action]
total_reward += reward
next_seq_in = np.identity(4)[len(seq) - 1]
next_state_in = np.identity(4)[action]
next_input = np.concatenate((next_seq_in, next_state_in))
next_input = next_input.reshape((1, 8))
next_output = model.predict(next_input)
if len(seq) < 4:
next_output_pos = np.take(next_output[0], togo)
else:
next_output_pos = np.take(next_output[0], [0])
target = reward + 0.9 * np.amin(next_output_pos)
output[0][action] = target
model.fit(input, output, epochs=1, verbose=0)
print(' ', len(seq) - 1, np.round(model.predict(input)[0], 3))
state = action
elif action == 0 or action == state:
target = 20
output[0][action] = target
model.fit(input, output, epochs=1, verbose=0)
if len(seq) == 4:
done = True
seq_in = np.identity(4)[len(seq) - 1]
state_in = np.identity(4)[state]
input = np.concatenate((seq_in, state_in))
input = input.reshape((1, 8))
action = 0
reward = time[state][action]
total_reward += reward
target = reward
output = np.ones((1, 4)) * 20
output[0][action] = target
model.fit(input, output, epochs=1, verbose=0)
print(' ', len(seq), np.round(model.predict(input)[0], 3))
seq.append(action)
print(i, seq, total_reward)
1 [32.773 32.064 32.774 33.274]
2 [30.603 33.861 33.241 33.526]
3 [32.036 32.797 33.014 33.469]
4 [31.835 33.828 32.97 33.839]
0 [0, 2, 1, 3, 0] 20
1 [32.78 32.307 33.006 33.181]
2 [32.083 33.619 33.514 33.777]
3 [29.785 32.65 32.229 32.314]
4 [31.231 33.4 32.429 33.231]
1 [0, 1, 2, 3, 0] 17
1 [32.467 32.25 32.778 32.896]
2 [31.426 33.257 32.935 33.185]
3 [29.219 32.272 31.712 31.782]
4 [30.671 32.998 31.915 32.708]
2 [0, 1, 2, 3, 0] 17
1 [32.14 32.144 32.531 32.655]
2 [30.957 33.618 33.413 33.502]
3 [30.077 31.408 31.344 31.588]
4 [28.104 31.855 29.982 30.568]
3 [0, 3, 1, 2, 0] 17
1 [31.517 31.798 32.139 32.204]
2 [28.448 32.544 31.603 31.48 ]
3 [29.506 30.975 30.932 31.112]
4 [29.356 31.961 30.868 31.527]
4 [0, 2, 1, 3, 0] 20
1 [31.145 31.575 31.939 31.929]
2 [29.623 31.908 31.522 31.588]
3 [27.507 30.985 30.403 30.253]
4 [28.924 31.608 30.515 31.122]
5 [0, 1, 2, 3, 0] 17
...
1 [20.054 15.438 17.223 15.806]
2 [19.92 20.21 11.178 12.799]
3 [19.803 10.01 19.01 7.2 ]
4 [ 3.959 18.949 19.914 21.557]
995 [0, 1, 2, 3, 0] 17
1 [19.994 15.775 17.356 15.47 ]
2 [19.986 9.682 17.074 20.3 ]
3 [19.872 10.057 19.302 7.033]
4 [ 3.007 21.345 18.947 19.158]
996 [0, 3, 2, 1, 0] 25
1 [20.053 15.816 17.687 15.395]
2 [19.986 20.175 11.477 12.565]
3 [19.93 9.92 19.613 7.011]
4 [ 4.005 18.99 20.286 21.318]
997 [0, 1, 2, 3, 0] 17
1 [20.077 15.891 17.826 15.373]
2 [19.99 20.144 11.498 12.498]
3 [19.947 9.927 19.697 6.946]
4 [ 4.002 19.046 20.279 21.211]
998 [0, 1, 2, 3, 0] 17
1 [20.086 16.015 17.78 15.302]
2 [20.124 12.955 21.238 9.685]
3 [19.866 5.715 14.834 18.025]
4 [ 3.041 21.327 18.964 18.839]
999 [0, 2, 3, 1, 0] 16
1 [20.161 16.101 17.538 15.153]
2 [20.043 20.128 11.24 12.311]
3 [19.965 5.64 14.804 18.108]
4 [ 3.908 19.862 21.357 18.255]
1000 [0, 1, 3, 2, 0] 21
1 [20.209 16.072 17.376 15.292]
2 [20.215 12.897 20.977 9.759]
3 [20.056 19.449 8.017 8.735]
4 [ 4.032 19.32 19.807 21.374]
1001 [0, 2, 1, 3, 0] 20
1 [20.023 16.486 16.86 15.424]
2 [20.003 13.474 20.745 9.851]
3 [19.849 6.113 14.243 18.197]
4 [ 2.965 21.743 18.764 19.216]
1002 [0, 2, 3, 1, 0] 16
1 [19.95 16.556 16.836 15.26 ]
2 [19.938 13.424 20.697 9.646]
3 [19.811 5.958 14.22 18.031]
4 [ 2.943 21.598 18.831 19.12 ]
1003 [0, 2, 3, 1, 0] 16
1 [19.933 16.392 16.818 15.114]
2 [19.804 20.628 10.902 12.423]
3 [19.857 10.185 19.157 6.577]
4 [ 3.984 19.015 19.827 21.032]
1004 [0, 1, 2, 3, 0] 17
1 [19.946 16.138 16.777 15.022]
2 [19.815 20.478 10.819 12.319]
3 [19.886 10.089 19.113 6.496]
4 [ 4.003 18.959 19.819 20.953]
1005 [0, 1, 2, 3, 0] 17
...
1 [19.73 15.056 14.511 14.715]
2 [19.905 11.149 20.292 7.234]
3 [20.061 4.695 12.859 19.974]
4 [ 2.997 19.993 20.003 19.999]
1995 [0, 2, 3, 1, 0] 16
1 [19.731 15.055 14.514 14.713]
2 [19.906 11.148 20.291 7.23 ]
3 [20.062 4.696 12.858 19.972]
4 [ 3. 19.996 20. 19.996]
1996 [0, 2, 3, 1, 0] 16
1 [19.732 15.057 14.511 14.71 ]
2 [19.907 11.15 20.288 7.226]
3 [20.063 4.7 12.855 19.971]
4 [ 3.002 20.002 19.997 19.997]
1997 [0, 2, 3, 1, 0] 16
1 [19.732 15.06 14.504 14.708]
2 [19.907 11.154 20.285 7.226]
3 [20.064 4.704 12.853 19.972]
4 [ 3.002 20.005 19.997 20. ]
1998 [0, 2, 3, 1, 0] 16
1 [19.732 15.06 14.5 14.71 ]
2 [19.906 11.154 20.285 7.23 ]
3 [20.063 4.704 12.853 19.974]
4 [ 3. 20.003 19.999 20.003]
1999 [0, 2, 3, 1, 0] 16
2000회의 반복적인 학습을 통해 얻은 Q-Network는 현재 상태를 나타내는 입력에 대한 Q-Value들을 출력하는데, Q-Table에서와 마찬가지로 이를 optimal policy로 사용할 수 있습니다.
위의 Q-Table의 Q-Value와 비교해보면 완전히 같지는 않지만 최소 이동 시간을 위한 경로를 선택하기에는 적합함을 알 수 있습니다.
Q-Network가 출력하는대로 가장 작은 값을 선택해서 D > 2 > 3 > 1 > D의 순서대로 이동하면 16이라는 (최소의) 총 이동 시간을 얻을 수 있습니다.