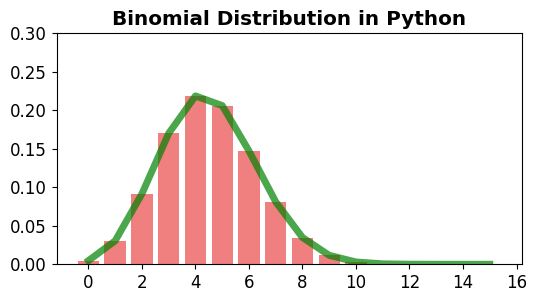
[확률과 통계] 파이썬으로 이항 분포 그리기¶
■ Table of Contents
1. 이항 분포란¶
이항 분포 (Binomial distribution)는 연속된 n번의 독립시행에서 각 시행이 성공할 (또는 일어날) 확률 p를 가질 때 만들어지는 이산 확률 분포입니다.
이 때 성공한 횟수를 X라는 확률변수로 나타내면, 확률변수 X는 이항 분포를 따르고 확률 질량 함수 (probability mass function)는 아래와 같이 주어집니다.
(이산 확률변수에 대한 확률 질량 함수는 연속 확률변수에 대해서 확률 밀도 함수 (probability density function)에 대응합니다.)
또한, 이항 분포의 평균, 분산, 표준편차는 각각 아래와 같이 주어집니다.
예를 들어, 15명의 환자에게 약을 투여해서 치료될 확률이 0.7이라고 할 때, 15명 중 5명의 환자가 치료될 확률은 아래와 같습니다.
또, 동전을 100회 던져서 앞면이 60회 나올 확률은 아래와 같습니다.
2. 이항 분포 그리기¶
위에서 설명한 이항 분포의 학률 함수를 파이썬과 NumPy, Matplotlib을 이용해서 그래프로 나타내보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from math import factorial
# Probability density of the binomial distribution
def bin_dist(k, n, p):
nck = factorial(n) / (factorial(k) * factorial(n - k))
pd = nck * p**k * (1-p)**(n-k)
return pd
x = np.arange(16)
pd1 = np.array([bin_dist(k, 15, 0.3) for k in range(16)])
plt.ylim(0, 0.3)
plt.text(12.5, 0.28, 'n, p = 15, 0.3')
plt.bar(x, pd1, color='lightcoral')
plt.show()
bin_dist(k, n, p) 함수는 p의 확률을 갖는 n회의 시행에서 k회 성공할 (일어날) 확률을 반환합니다.
x는 0에서 15까지의 정수값을 갖는 NumPy 어레이이고, pd1은 각 x값에 대한 확률 질량 함수의 값을 갖는 어레이입니다.
plt.ylim(a, b)은 y축의 범위를 a에서 b으로 지정합니다.
plt.text(x, y, s)는 x, y의 위치에 문자열 s를 나타냅니다. x와 y는 그래프 x, y축 상의 값입니다.
plt.bar()는 x, y 데이터를 막대그래프로 나타냅니다.
결과는 아래와 같습니다.
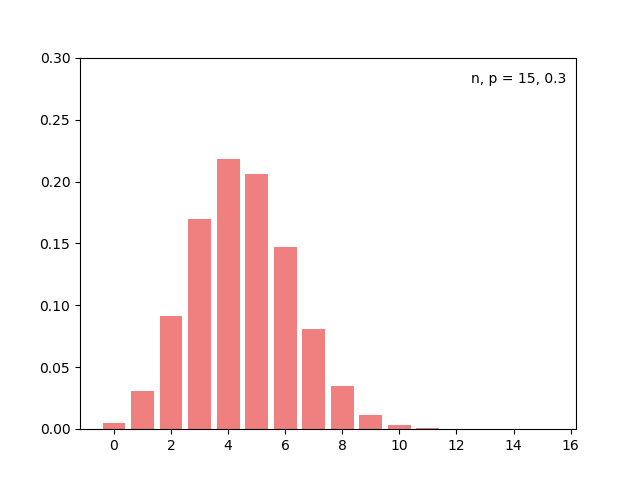
n, p = 15, 0.3일 때의 확률질량함수.¶
3. 사건이 일어날 확률¶
이항 분포는 시행의 횟수 n과 사건이 일어날 확률 p에 의해 결정됩니다.
아래의 예제에서는 사건이 일어날 확률 p가 0.3, 0.5, 0.7로 달라질 때, 확률 질량 함수의 변화를 그래프로 나타냅니다.
import numpy as np
import matplotlib.pyplot as plt
from math import factorial
# Probability density of the binomial distribution
def bin_dist(k, n, p):
nck = factorial(n) / (factorial(k) * factorial(n - k))
pd = nck * p**k * (1-p)**(n-k)
return pd
x = np.arange(16)
pd1 = np.array([bin_dist(k, 15, 0.3) for k in range(16)])
plt.subplot(3, 1, 1)
plt.ylim(0, 0.3)
plt.text(12.5, 0.25, 'n, p = 15, 0.3')
plt.bar(x, pd1, color='lightcoral')
pd2 = np.array([bin_dist(k, 15, 0.5) for k in range(16)])
plt.subplot(3, 1, 2)
plt.ylim(0, 0.3)
plt.text(12.5, 0.25, 'n, p = 15, 0.5')
plt.bar(x, pd2, color='mediumaquamarine')
pd3 = np.array([bin_dist(k, 15, 0.7) for k in range(16)])
plt.subplot(3, 1, 3)
plt.ylim(0, 0.3)
plt.text(12.5, 0.25, 'n, p = 15, 0.7')
plt.bar(x, pd3, color='royalblue')
plt.show()
pd1, pd2, pd3은 각각 n=15이고, p=0.3, 0.5, 0.7일 때의 확률 질량 함수를 나타냅니다.
결과는 아래와 같습니다.
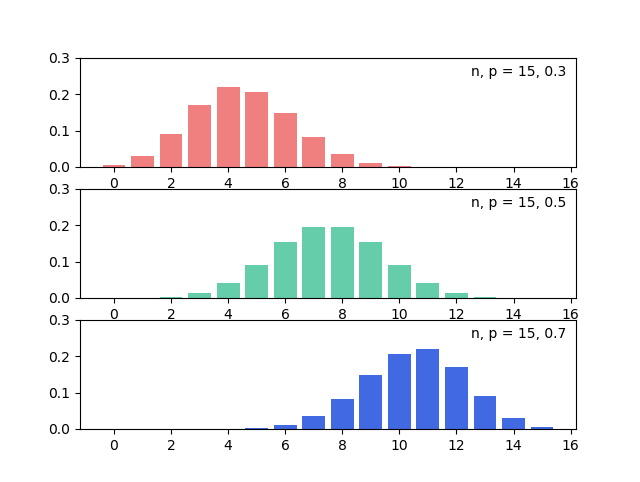
n = 15, p = 0.3, 0.5, 0.7일 때의 확률 질량 함수.¶
4. np.random.binomial()¶
NumPy random 모듈의 random.binomial() 함수는 이항 분포로부터 얻은 임의의 샘플을 반환합니다.
import numpy as np
np.random.seed(0)
n, p = 15, 0.3
s = np.random.binomial(n, p, 100)
print(s)
[5 5 5 5 4 5 4 7 8 4 6 5 5 7 2 2 1 6 6 7 8 6 4 6 2 5 3 7 5 4 3 6 4 5 1 5 5
5 7 5 4 4 5 2 5 5 3 3 4 4 5 4 9 2 3 3 5 3 4 3 3 2 5 3 3 4 6 2 6 2 8 4 8 5
6 2 3 2 3 2 4 4 2 5 5 3 5 2 5 7 4 5 3 5 3 3 5 1 6 0]
n, p = 15, 0.3인 이항분포를 따르는 임의의 정수가 100개 만들어집니다.
이제 p를 0.3, 0.5 0.7로 변화시키면서 그래프로 나타내보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
s1 = np.random.binomial(15, 0.3, 1000)
s2 = np.random.binomial(15, 0.5, 1000)
s3 = np.random.binomial(15, 0.7, 1000)
plt.subplot(3, 1, 1)
plt.xlim(0, 16)
plt.ylim(0, 300)
plt.text(12.5, 250, 'n, p = 15, 0.3')
plt.hist(s1, color='lightcoral')
plt.subplot(3, 1, 2)
plt.xlim(0, 16)
plt.ylim(0, 300)
plt.text(12.5, 250, 'n, p = 15, 0.5')
plt.hist(s2, color='mediumaquamarine')
plt.subplot(3, 1, 3)
plt.xlim(0, 16)
plt.ylim(0, 300)
plt.text(12.5, 250, 'n, p = 15, 0.7')
plt.hist(s3, color='royalblue')
plt.show()
결과는 아래와 같습니다.
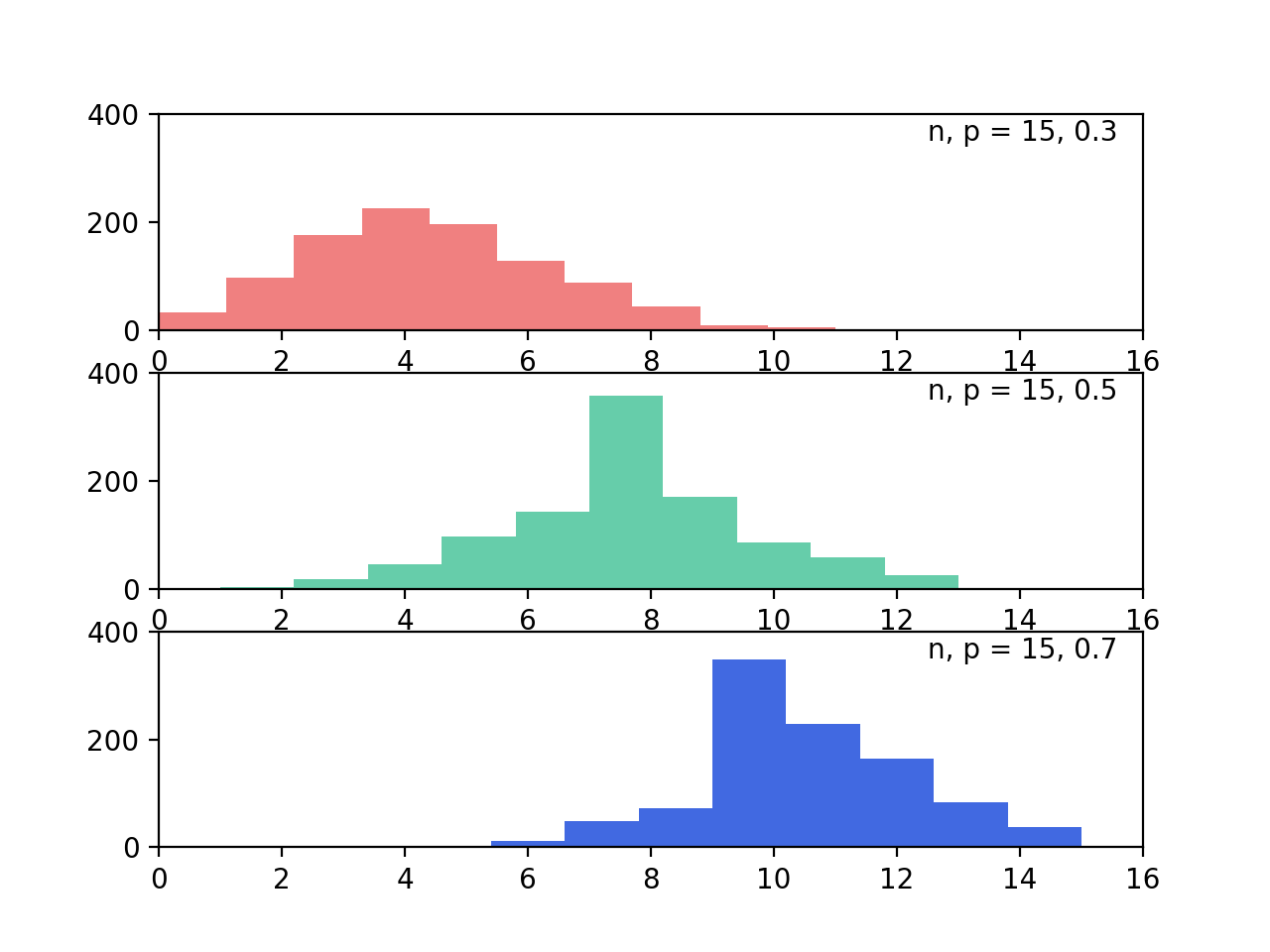
n = 15, p = 0.3, 0.5, 0.7일 때의 사건이 일어난 횟수의 분포 (1000개의 난수 생성).¶