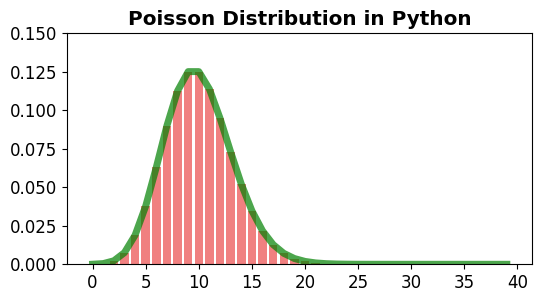
[확률과 통계] 파이썬으로 푸아송 분포 그리기¶
■ Table of Contents
1. 푸아송 분포란¶
푸아송 분포 (Poisson distribution)는 단위 시간 안에 어떤 사건이 몇 번 일어날 것인지를 표현하는 이산 확률 분포입니다.
프랑스의 수학자이자 물리학자인 시메옹 드니 푸아송 (Siméon Denis Poisson)이 저서 ‘민사 사건과 형사 사건 재판에서의 확률에 관한 연구 및 일반적인 확률 계산 법칙에 대한 서문’에서 최초로 사용하였습니다.
푸아송 분포에서, 정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기대값이 \(\lambda\)라고 했을 때, 그 사건이 n회 일어날 확률은 아래와 같이 주어집니다.
푸아송 분포는 동일한 크기의 어떤 (시간 또는 공간) 구간에서 사건 발생 확률이 동일하고,
각 사건이 일어날 확률이 다른 사건이 일어날 확률과 서로 독립적일 때 적용할 수 있습니다.
푸아송 분포의 평균과 분산은 아래와 같이 모두 \(\lambda\)로 주어집니다.
예를 들어, 어떤 식당에 주말 오후 동안 시간당 평균 20명의 손님이 방문한다고 할 때, 다음주 주말 오후에 30분 동안 5명의 손님이 방문할 확률은 아래와 같습니다. (시간당 평균 20명이 방문하므로, 30분당 기대값은 10명.)
2. 푸아송 분포 그리기¶
위에서 설명한 푸아송 분포의 학률 함수를 파이썬과 NumPy, Matplotlib을 이용해서 그래프로 나타내보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from math import factorial, exp
# Probability density of the Poisson distribution
def pois_dist(n, lamb):
pd = (lamb ** n) * exp(-lamb) / factorial(n)
return pd
x = np.arange(40)
pd1 = np.array([pois_dist(n, 10) for n in range(40)])
plt.ylim(0, 0.15)
plt.text(33.5, 0.14, 'lamb = 10')
plt.bar(x, pd1, color='lightcoral')
plt.show()
pois_dist(n, lamb) 함수는 기대값 lamb을 가질 때, n회의 사건이 일어날 확률을 반환합니다.
x는 0에서 39까지의 정수값을 갖는 NumPy 어레이이고, pd1은 각 x값에 대한 확률 질량 함수의 값을 갖는 어레이입니다.
plt.ylim(a, b)은 y축의 범위를 a에서 b으로 지정합니다.
plt.text(x, y, s)는 x, y의 위치에 문자열 s를 나타냅니다. x와 y는 그래프 x, y축 상의 값입니다.
plt.bar()는 x, y 데이터를 막대그래프로 나타냅니다.
결과는 아래와 같습니다.
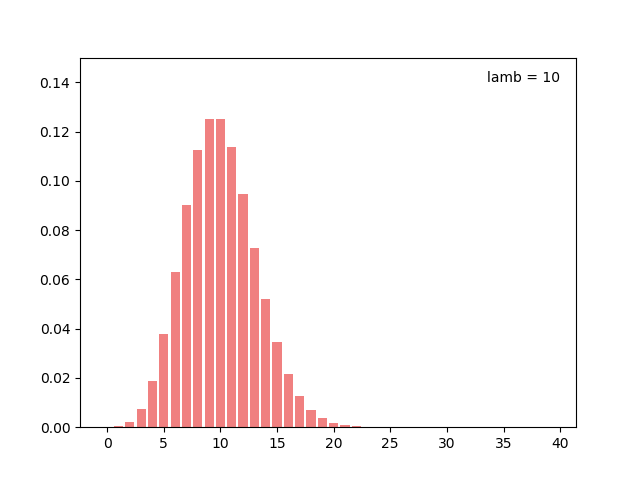
lamd = 10일 때의 확률질량함수.¶
3. 사건의 기대값 \(\lambda\)¶
푸아송 분포는 어떤 기간 동안 (또는 어떤 공간 내에서) 사건이 일어날 기대값에 의해 결정됩니다.
아래의 예제에서는 사건의 기대값이 10, 15, 20으로 변화할때, 확률 질량 함수의 변화를 그래프로 나타냅니다.
import numpy as np
import matplotlib.pyplot as plt
from math import factorial, exp
# Probability density of the Poisson distribution
def pois_dist(n, lamb):
pd = (lamb ** n) * exp(-lamb) / factorial(n)
return pd
x = np.arange(40)
plt.subplot(3, 1, 1)
pd1 = np.array([pois_dist(n, 10) for n in range(40)])
plt.ylim(0, 0.15)
plt.text(33.5, 0.12, 'lamb = 10')
plt.bar(x, pd1, color='lightcoral')
plt.subplot(3, 1, 2)
pd2 = np.array([pois_dist(n, 15) for n in range(40)])
plt.ylim(0, 0.15)
plt.text(33.5, 0.12, 'lamb = 15')
plt.bar(x, pd2, color='mediumaquamarine')
plt.subplot(3, 1, 3)
pd3 = np.array([pois_dist(n, 20) for n in range(40)])
plt.ylim(0, 0.15)
plt.text(33.5, 0.12, 'lamb = 20')
plt.bar(x, pd3, color='royalblue')
plt.show()
pd1, pd2, pd3은 각각 기대값 \(\lambda\) = 10, 15, 20일 때의 확률 질량 함수를 나타냅니다.
결과는 아래와 같습니다.
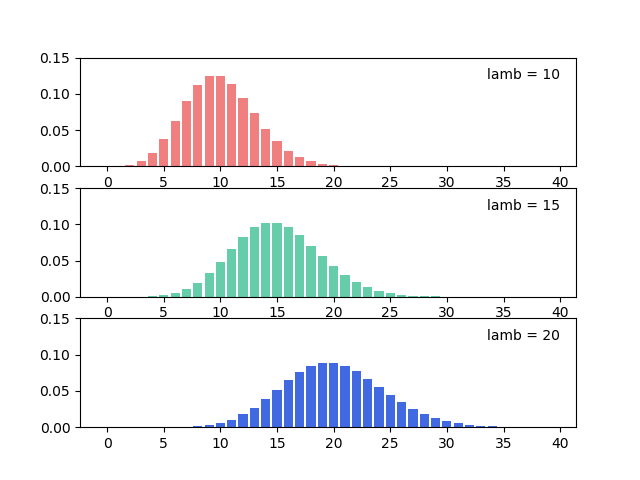
lamb = 10, 15, 20일 때의 확률 질량 함수.¶
\(\lambda\)가 증가하면서, 푸아송 분포의 평균과 분산도 함께 증가하는 것을 알 수 있습니다.