파이썬으로 Random Walk 구현하기¶

Random walk (무작위 행보)는 수학, 물리학, 컴퓨터 과학 분야에서 임의의 방향으로 움직이는 연속적인 값을 나타내는 개념입니다.

예를 들어, 아래 그림과 같이 비틀거리는 취객의 예측하기 어려운 움직임을 표현하기 위해 Random walk 모델을 사용할 수 있습니다.

Random walk 모델의 예: 취객의 움직임. (이미지 참고)¶

Random walk 모델에서 시간에 따른 편차의 평균은 0이고 분산은 시간에 비례해서 증가합니다.

따라서 좌/우 또는 앞/뒤로 움직일 확률이 동일하다고 해도 시간의 흐름에 따라 평균에서 점차 벗어나는 경향을 보입니다.

이 페이지에서는 파이썬과 NumPy 패키지를 이용해서 Random walk 모델을 구현해 보겠습니다.

순서는 아래와 같습니다.

시간 데이터 만들기
Random 데이터 만들기
여러개의 Random 데이터 만들기
틱 (tick) 조절하기
평균/표준편차 조절하기
관련 페이지

시간 데이터 만들기¶

import matplotlib.pyplot as plt
import numpy as np
import datetime
from datetime import timedelta

np.random.seed(1)

# 1분 단위 Time series 생성
init_time = datetime.datetime(2020, 4, 1, 9, 0, 0)      # 2020-04-01 09:00:00
time_series = np.array([init_time])
for i in range(120):
    new_time = time_series[-1] + timedelta(minutes=1)
    time_series = np.append(time_series, new_time)

print(time_series[0])
print(time_series[-1])

2020-04-01 09:00:00
2020-04-01 11:00:00

시간 데이터를 만들기 위해 파이썬의 datetime 모듈을 사용합니다.

init_time은 날짜/시간 (2020-04-01 09:00:00)을 나타내는 datetime 클래스입니다.

time_series는 시간 데이터를 저장할 NumPy 어레이입니다.

timedelta(minutes=1)을 이용해서 1분 단위의 시간을 더한 datetime 클래스를 time_series 어레이에 추가해줍니다.

결과를 출력해보면 2020-04-01 09:00:00부터 2020-04-01 11:00:00까지의 datetime 클래스가 생성된 것을 알 수 있습니다.

Random 데이터 만들기¶

이제 이 시간 데이터에 따라 무작위로 움직이는 데이터를 만들어 보겠습니다.

init_data = 10000
tick = 100
random_data_series = np.array([init_data])
for i in range(120):
    new_data = random_data_series[-1] + tick * np.around(np.random.randn())
    random_data_series = np.append(random_data_series, new_data)

print(random_data_series)

plt.plot(time_series, random_data_series)
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()

[10000. 10200. 10100. 10000.  9900. 10000.  9800. 10000.  9900.  9900.
10000.  9800.  9800.  9800.  9900.  9800.  9800.  9700.  9700.
 9700.  9800.  9900. 10000. 10100. 10000. 10000.  9900.  9900.
 9900.  9900.  9800.  9700.  9600.  9600.  9500.  9500.  9700.
 9800.  9700.  9600.  9800.  9800.  9700.  9700.  9900.  9900.
10000. 10000.  9900.  9900.  9900. 10000. 10100. 10200. 10200.
10200. 10300. 10400. 10400. 10400. 10400. 10500. 10700. 10900.
10700. 10600. 10600. 10700. 10700. 10500. 10500. 10600. 10600.
10700. 10700. 10700. 10700. 10700. 10700. 10600. 10600. 10600.
10800. 10800. 10800. 10700. 10700. 10700. 10700. 10700. 10600.
10700. 10800. 10800. 10900. 10800. 10800. 10900. 10800. 10800.
10700. 10700. 10800. 10700. 10700. 10600. 10600. 10400. 10500.
]

10000에서 시작해서 임의의 방향으로 움직이는 120개의 데이터를 만들었습니다.

init_data = 10000
tick = 100
random_data_series = np.array([init_data])

init_data와 tick은 데이터의 초기값과 움직이는 폭을 나타내는 변수입니다.

random_data_series는 임의로 만들어지는 데이터를 저장하는 NumPy 어레이입니다.

new_data = random_data_series[-1] + tick * np.around(np.random.randn())
random_data_series = np.append(random_data_series, new_data)

np.random.randn()은 표준정규분포를 갖는 난수를 반환합니다.

np.around()는 주어진 소수점 자리로 반올림을 하는 함수입니다.

숫자가 주어지지 않을 경우 정수가 됩니다. (Default=0)

표준정규분포를 갖는 임의의 정수에 tick을 곱해서 random_data_series의 마지막 데이터에 더해줍니다.

Matplotlib을 이용해서 그래프로 나타내보면 아래 그림과 같습니다.

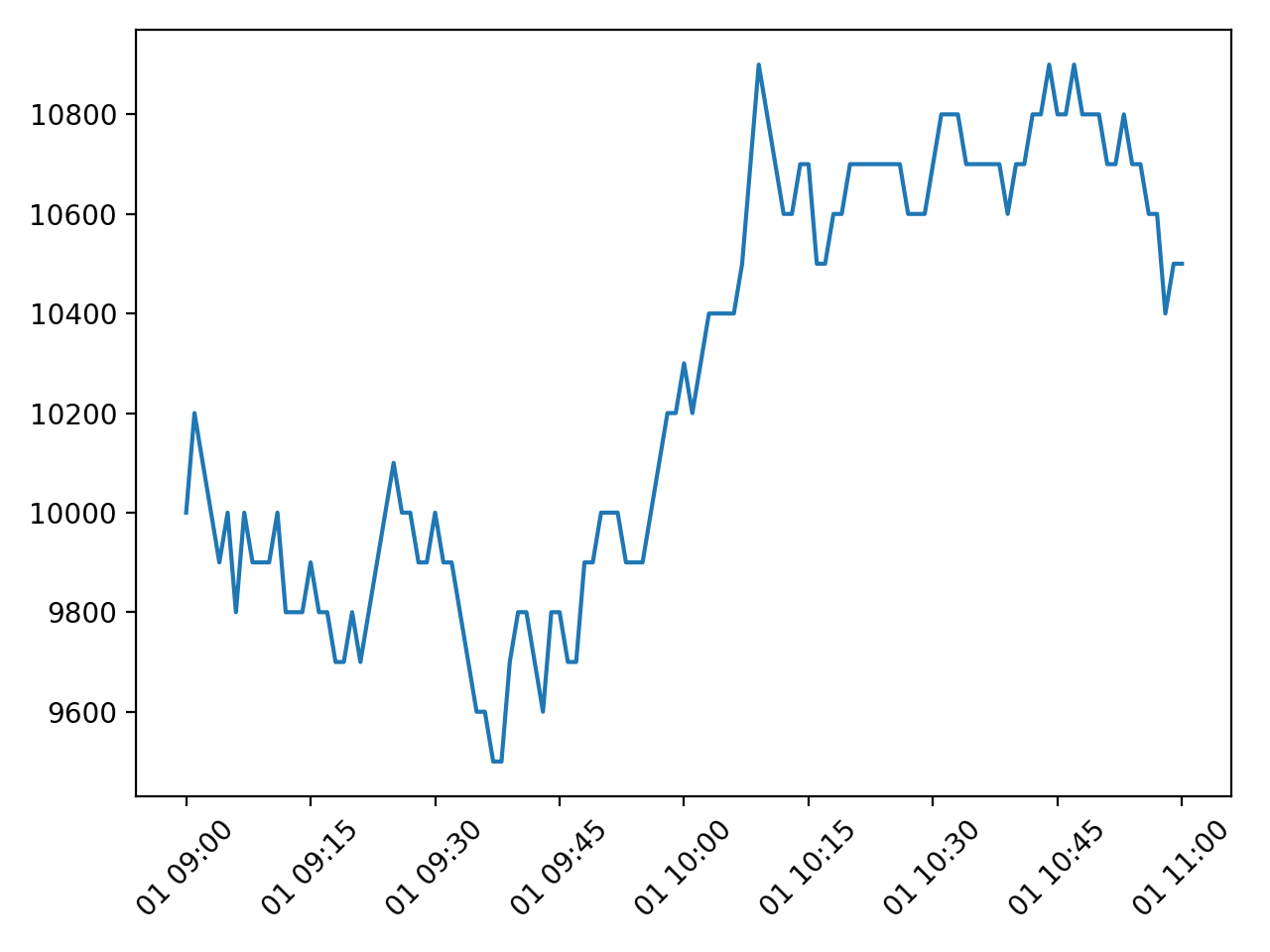
Random walk 모델로 생성된 데이터.¶

초기값 10000에서 시작해서 120분 동안 100 단위로 무작위로 움직이는 데이터가 만들어졌습니다.

여러개의 Random 데이터 만들기¶

Random한 움직임을 보이는 데이터를 100번의 시행을 통해 만들어 보겠습니다.

import matplotlib.pyplot as plt
import numpy as np
import datetime
from datetime import timedelta

np.random.seed(1)

# 1분 단위 Time series 생성
init_time = datetime.datetime(2020, 4, 1, 9, 0, 0)      # 2020-04-01 09:00:00
time_series = np.array([init_time])
for i in range(120):
  new_time = time_series[-1] + timedelta(minutes=1)
  time_series = np.append(time_series, new_time)

arr_rd = []
for n in range(100):
  init_data = 10000
  tick = 100
  random_data_series = np.array([init_data])
  # Random data 생성
  for i in range(120):
      new_data = random_data_series[-1] + tick * np.around(np.random.randn())
      random_data_series = np.append(random_data_series, new_data)
  arr_rd.append(random_data_series)
  plt.plot(time_series, random_data_series, alpha=0.5)

plt.xticks(rotation=45)
plt.tight_layout()
plt.show()

Random walk 모델을 사용한 데이터를 100회 생성해서 arr_rd에 저장하고 그래프로 나타냈습니다.

결과는 아래와 같습니다.

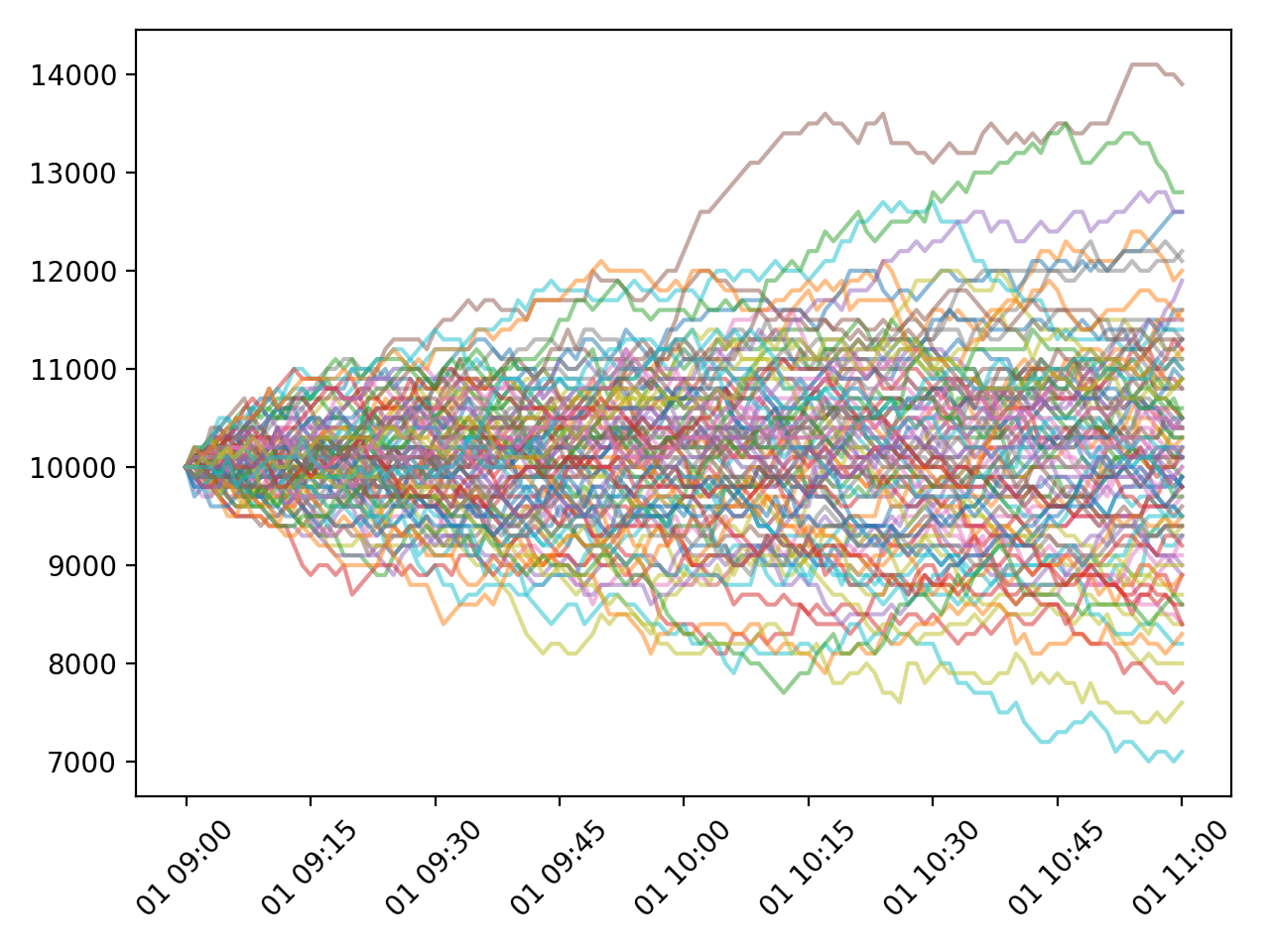
Random walk 모델로 생성된 100개의 데이터.¶

틱 (tick) 조절하기¶

tick을 두 배로 증가시켜서 Random walk 데이터를 생성해보겠습니다.

tick = 200

tick 변수를 200으로 수정합니다.

결과는 아래와 같습니다.

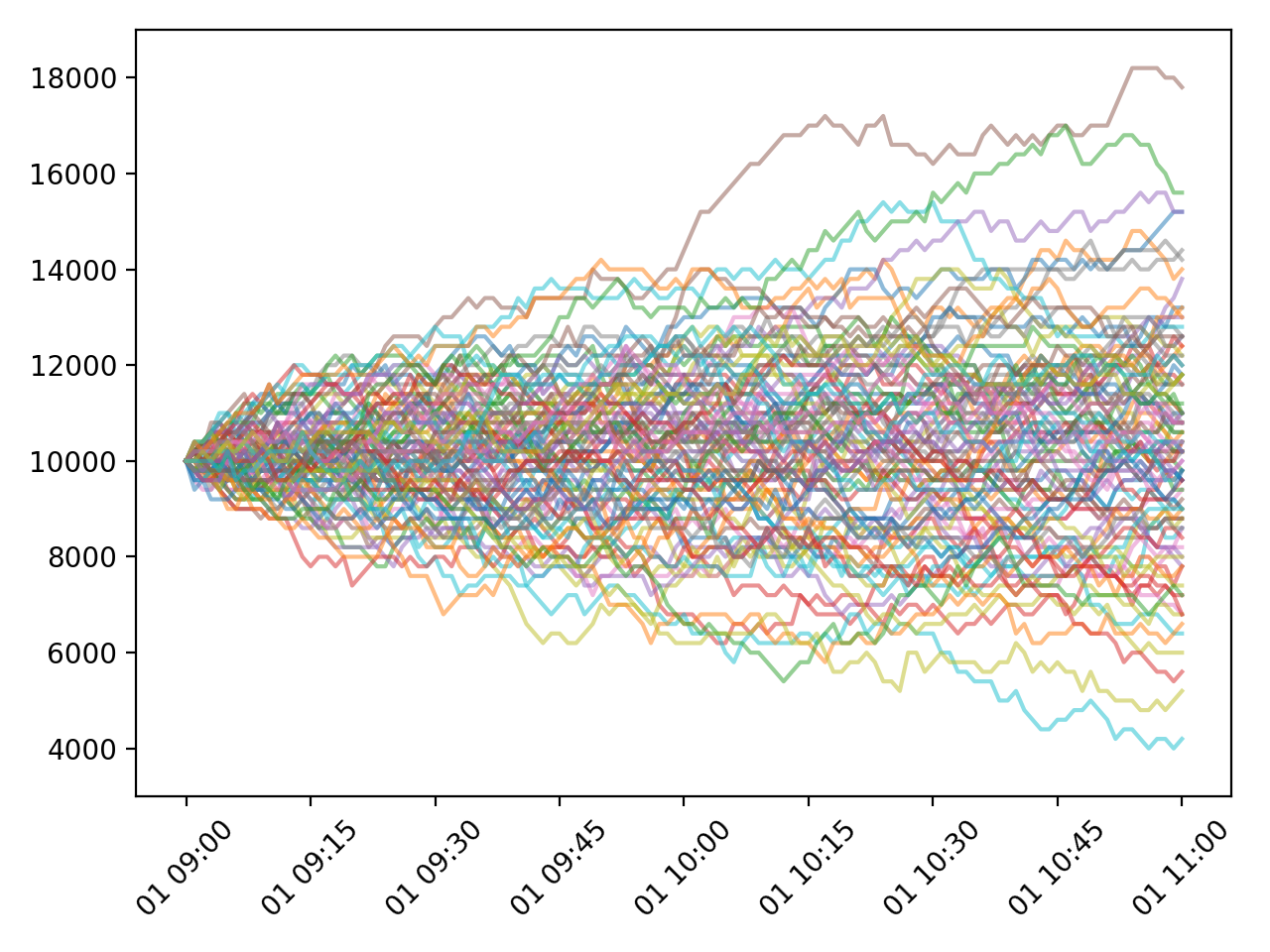
Random walk 모델로 생성된 100개의 데이터 (tick=200).¶

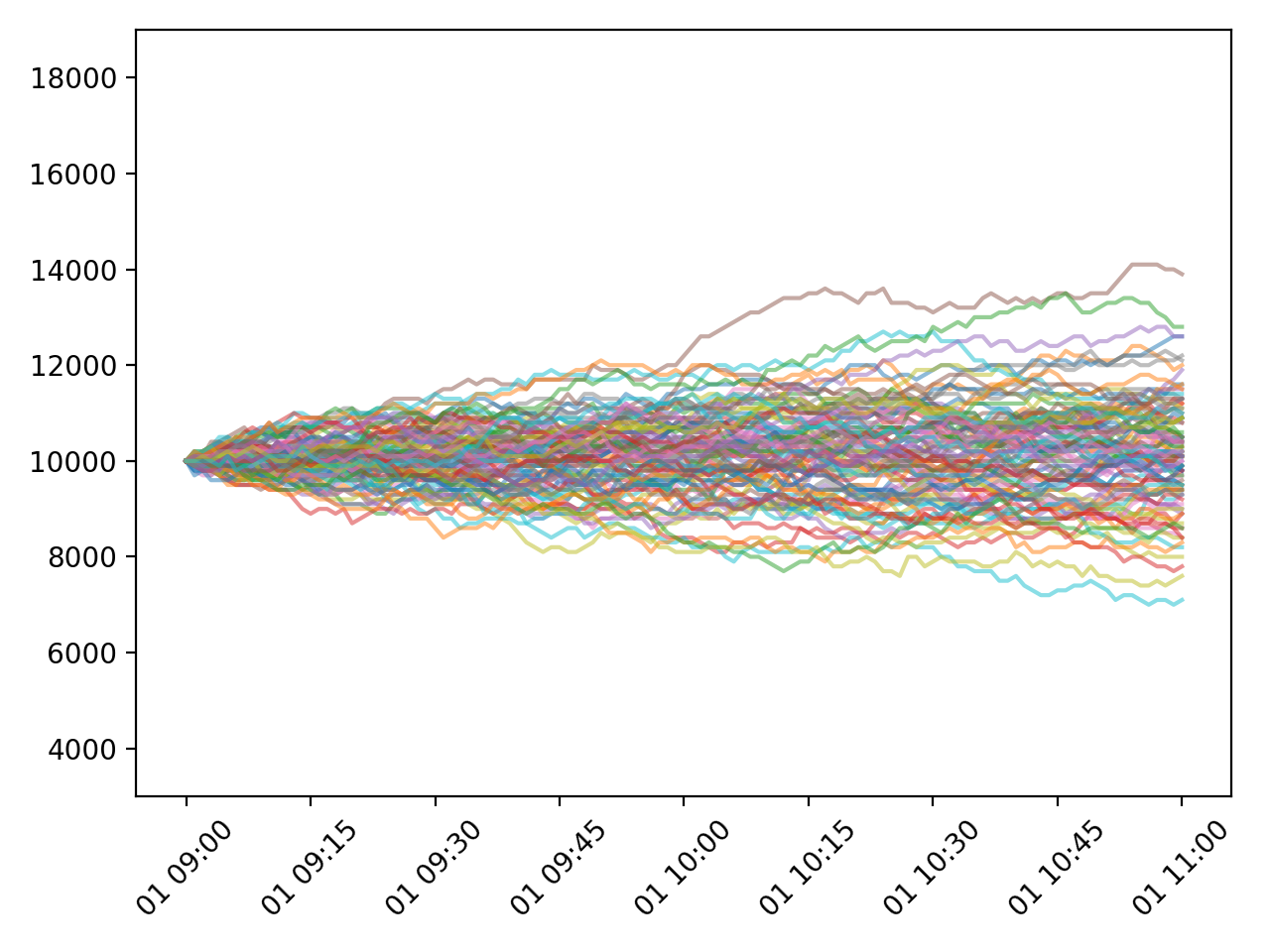
Random walk 모델로 생성된 100개의 데이터 (tick=100).¶

plt.ylim()을 이용해서 y축을 동일하게 하고 tick이 100인 경우와 비교하면 편차의 범위가 tick의 크기에 비례해서 증가한 것을 알 수 있습니다.

평균/표준편차 조절하기¶

표준정규분포 상에서 Random하게 만들어지는 데이터에 평균과 표준편차를 조절해서 바이어스를 반영할 수 있습니다.

new_data = random_data_series[-1] + tick * np.around(2.0 * np.random.randn() + 0.5)

표준정규분포 N(1, 0)이 아닌, 평균 \({\mu}\), 표준편차 \({\sigma}\) 를 갖는 정규분포 N(\({\mu}\), \({\sigma}\)²)의 난수를 원한다면

\({\sigma}\) * np.random.randn(…) + \({\mu}\) 와 같은 형태로 사용합니다.

평균을 0.5로 표준편차를 2로 조절했습니다. (참고 - NumPy 난수 생성 (Random 모듈))

만들어진 데이터의 움직임은 아래 그림과 같습니다.

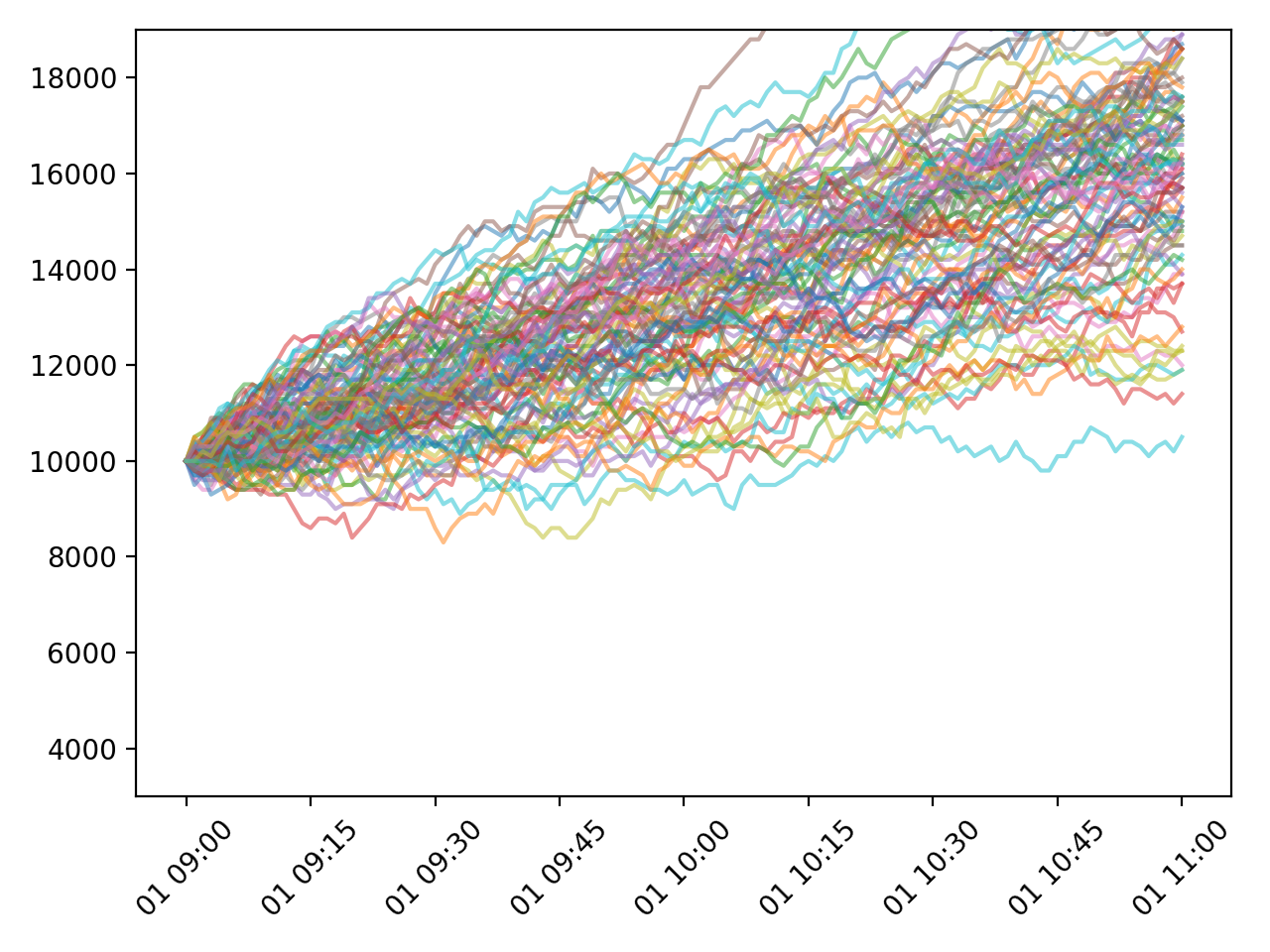
평균과 표준편차를 조절한 Random walk 모델로 생성된 100개의 데이터 (\({\mu}=0.5\), \({\sigma}=2.0\), tick=100).¶

Random walk 모델로 생성된 100개의 데이터 (\({\mu}=0.0\), \({\sigma}=1.0\), tick=100).¶

평균과 표준편차가 0.0, 1.0인 데이터와 비교하면 편차가 커지고 상승하는 형태의 움직임을 보임을 알 수 있습니다.