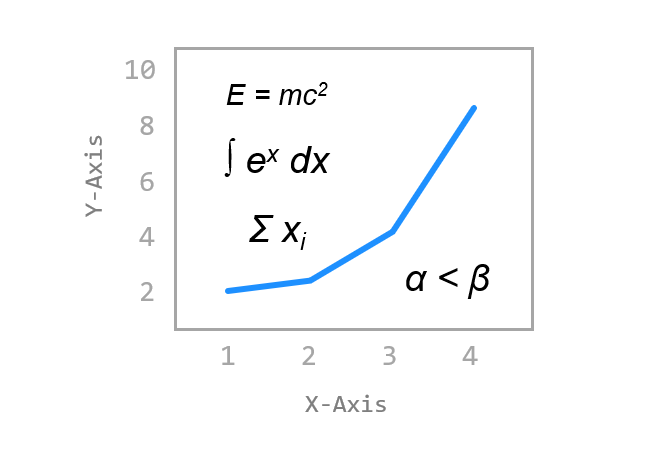Matplotlib 수학적 표현 사용하기

달러 기호 ($) 사이에 위치하는 TeX 마크업 표현을 통해 Matplotlib에서 수학적 표현을 사용할 수 있습니다.

그래프의 제목, 축 레이블, 그리고 데이터 곡선을 설명하는 텍스트 상자에도 수학적 표현을 사용할 수 있습니다.

이 페이지에서는 Matplotlib 그래프에서 다양한 수학적 표현을 사용하는 방법에 대해 소개합니다.

Keyworkd: 수학적 표현, 특수 문자, 첨자, 분수

1) 그리스 문자 (Greek Letter)

Matplotlib에서 문자열에 수학적 표현을 사용하기 위해서 아래와 같이 세가지 표현이 필요합니다.

• ‘r’은 파이썬 문자열을 raw string으로 표현하도록 합니다.

• Matplotlib의 수학적 표현은 두 개의 달러 기호 ($) 사이에 위치해야 합니다.

• Tex 마크업 언어 (참고)를 사용해서 각각의 수학적 표현과 기호를 사용합니다.

예제

import matplotlib.pyplot as plt

plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.xlabel('X-Label')
plt.ylabel('Y-Label')
plt.text(1, 15, r'$\alpha > \beta$', fontdict={'size': 16})

plt.show()

text() 함수를 사용해서 그래프의 x=1, y=15 위치에 그리스 문자를 포함하는 문자열을 삽입했습니다.

아래 그림과 같이 그래프에 \(\alpha\)와 \(\beta\)가 표시됩니다.

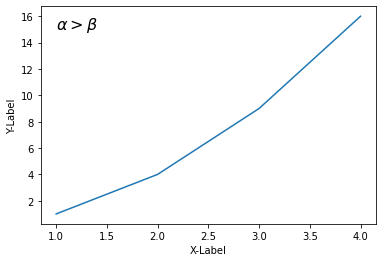
Matplotlib 수학적 표현 나타내기 - 그리스 문자

그리스 문자를 위한 TeX 기호는 아래의 표를 참고하세요.

소문자

\(\alpha\) \alpha	\(\beta\) \beta	\(\chi\) \chi	\(\delta\) \delta	\(\digamma\) \digamma	\(\epsilon\) \epsilon
\(\eta\) \eta	\(\gamma\) \gamma	\(\iota\) \iota	\(\kappa\) \kappa	\(\lambda\) \lambda	\(\mu\) \mu
\(\nu\) \nu	\(\omega\) \omega	\(\phi\) \phi	\(\pi\) \pi	\(\psi\) \psi	\(\rho\) \rho
\(\sigma\) \sigma	\(\tau\) \tau	\(\theta\) \theta	\(\upsilon\) \upsilon	\(\varepsilon\) \varepsilon	\(\varkappa\) \varkappa
\(\varphi\) \varphi	\(\varpi\) \varpi	\(\varrho\) \varrho	\(\varsigma\) \varsigma	\(\vartheta\) \vartheta	\(\xi\) \xi
\(\zeta\) \zeta

대문자

\(\Delta\) \Delta	\(\Gamma\) \Gamma	\(\Lambda\) \Lambda	\(\Omega\) \Omega	\(\Phi\) \Phi	\(\Pi\) \Pi
\(\Psi\) \Psi	\(\Sigma\) \Sigma	\(\Theta\) \Theta	\(\Upsilon\) \Upsilon	\(\Xi\) \Xi	\(\mho\) \mho
\(\nabla\) \nabla

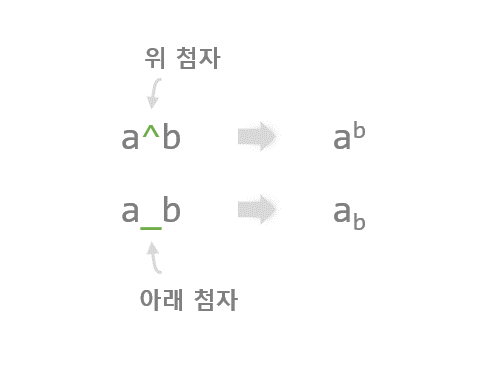
2) 위 첨자 (Superscripts), 아래 첨자 (Subscripts)

위 첨자와 아래 첨자를 위해서는 아래와 같이 각각 ‘^’와 ‘_’ 기호를 사용합니다.

예제

import matplotlib.pyplot as plt

plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.xlabel('X-Label')
plt.ylabel('Y-Label')
plt.text(1, 15, r'$\alpha^2 > \beta_5$', fontdict={'size': 16})

plt.show()

‘^’와 ‘_’를 사용해서 그래프에 위 첨자와 아래 첨자를 포함하는 수식 표현을 삽입했습니다.

결과는 아래와 같습니다.

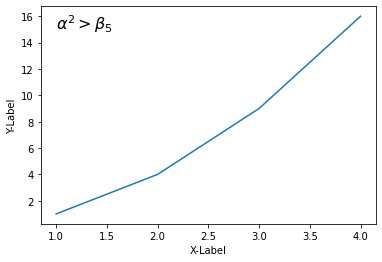
Matplotlib 수학적 표현 나타내기 - 위 첨자 (Superscripts), 아래 첨자 (Subscripts)

3) 분수 (Fractions)

분수 표현을 사용하기 위해서는 아래와 같이 \frac{ }{ } 표현을 사용합니다.

예제

import matplotlib.pyplot as plt

plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.xlabel('X-Label')
plt.ylabel('Y-Label')
plt.text(1, 15, r'$\frac{1}{2} + \frac{3}{4} = \frac{5}{4}$', fontdict={'size': 16})

plt.show()

아래와 같이 그래프에 분수 표현 수식이 삽입되었습니다.

Matplotlib 수학적 표현 나타내기 - 분수 (Fractions)

4) 거듭제곱 근호 (Radical Signs)

거듭제곱 근호를 표현하기 위해서는 \sqrt{ } 또는 \sqrt[ ]{ }를 사용합니다.

예제

import matplotlib.pyplot as plt

plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.xlabel('X-Label')
plt.ylabel('Y-Label')
plt.text(1, 15, r'$\sqrt{2} + \sqrt[3]{x} = y$', fontdict={'size': 16})

plt.show()

아래와 같이 그래프에 근호를 포함한 수식이 삽입되었습니다.

Matplotlib 수학적 표현 나타내기 - 거듭제곱 근호 (Radical Signs)

5) 액센트 (Accents)

액센트는 강세, 억양을 나타내거나 수학적 표현을 위해 문자의 위에 표시되는 기호입니다.

Matplotlib에서 액센트를 사용하기 위해서는 아래와 같이 \acute, \bar 등의 TeX 기호를 함께 사용합니다.

예제

import matplotlib.pyplot as plt

plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.xlabel('X-Label')
plt.ylabel('Y-Label')
plt.text(1, 15, r'$\acute a, \bar a, \tilde a$', fontdict={'size': 16})
plt.text(1, 13, r'$\vec a \cdot \vec a = |\vec a|^2$', fontdict={'size': 16})
plt.text(1, 11, r'$\overline{abc}$', fontdict={'size': 16})

plt.show()

다양한 액센트 기호를 포함하는 문자열을 그래프에 나타냈습니다.

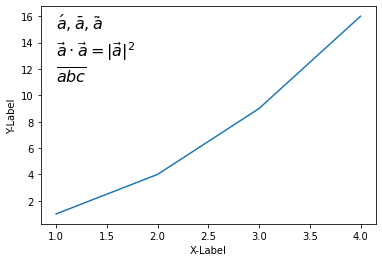
Matplotlib 수학적 표현 나타내기 - 액센트 (Accents)

더 다양한 액센트 기호는 아래의 표를 참고하세요.

Command	Result	Command	Result	Command	Result	Command	Result
\acute a	\(\acute a\)	\bar a	\(\bar a\)	\breve a	\(\breve a\)	\ddot a	\(\ddot a\)
\dot a	\(\dot a\)	\grave a	\(\grave a\)	\hat a	\(\hat a\)	\tilde a	\(\tilde a\)
\vec a	\(\vec a\)	\overline{abc}	\(\overline{abc}\)	\widehat{abc}	\(\widehat{abc}\)	\widetilde{abc}	\(\widetilde{abc}\)

6) 표준 함수 (Standard Functions)와 대형 기호 (Big Symbols)

아래 그림과 같이 Matplotlib에서 삼각함수 (sin, cos, tan 등), 극한 (lim), 최대 (max), 최소 (min) 등의 표현과

다양한 대형 연산자 기호를 사용할 수 있습니다.

예제

import matplotlib.pyplot as plt

plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.xlabel('X-Label')
plt.ylabel('Y-Label')
plt.text(1, 15, r'$\sin (x) \ \cos (x) \ \tan (x)$', fontdict={'size': 16})
plt.text(1, 12, r'$\lim_{x\rightarrow 2} (x^2 - x + 2)$', fontdict={'size': 16})
plt.text(1, 8, r'$\sum_{n=0}^{10}{(n^2 + n)}$', fontdict={'size': 16})
plt.show()

그래프에 여러가지 삼각함수와 극한 기호, 그리고 합 기호 (Summation symbol)를 표시했습니다.

결과는 아래와 같습니다.

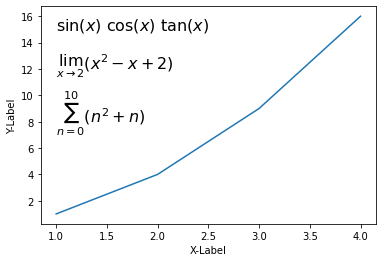
Matplotlib 수학적 표현 나타내기 - 표준 함수 (Standard Functions)와 대형 기호 (Big Symbols)

더 다양한 표준 함수의 기호는 아래의 표를 참고하세요.

Command	Result	Command	Result	Command	Result	Command	Result
\Pr	\(\Pr\)	\arccos	\(\arccos\)	\arcsin	\(\arcsin\)	\arctan	\(\arctan\)
\arg	\(\arg\)	\cos	\(\cos\)	\cosh	\(\cosh\)	\cot	\(\cot\)
\coth	\(\coth\)	\csc	\(\csc\)	\deg	\(\deg\)	\det	\(\det\)
\dim	\(dim\)	\exp	\(\exp\)	\gcd	\(\gcd\)	\hom	\(\hom\)
\inf	\(\inf\)	\ker	\(\ker\)	\lg	\(\lg\)	\lim	\(\lim\)
\liminf	\(\liminf\)	\limsup	\(\limsup\)	\ln	\(\ln\)	\log	\(\log\)
\max	\(\max\)	\min	\(\min\)	\sec	\(\sec\)	\sin	\(\sin\)
\sinh	\(\sinh\)	\sup	\(\sup\)	\tan	\(\tan\)	\tanh	\(\tanh\)

대형 기호는 아래의 표를 참고하세요.

Command	Result	Command	Result	Command	Result	Command	Result
\bigcap	\(\bigcap\)	\bigcup	\(\bigcup\)	\bigodot	\(\bigodot\)	\bigoplus	\(\bigoplus\)
\bigotimes	\(\bigotimes\)	\biguplus	\(\biguplus\)	\bigvee	\(\bigvee\)	\bigwedge	\(\bigwedge\)
\coprod	\(\coprod\)	\int	\(\int\)	\oint	\(\oint\)	\prod	\(\prod\)
\sum	\(\sum\)

그리고 더 다양한 수학적 표현의 사용과 그 설명에 대해서는 공식 문서의 설명 (링크)을 참고하세요.

이전글/다음글

이전글 : Matplotlib 텍스트 삽입하기

다음글 : Matplotlib 그래프 스타일 설정하기

공유하기