2. 간단한 신경망 만들기

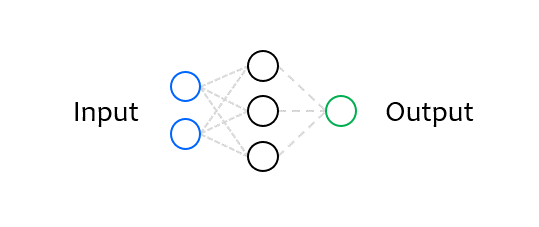
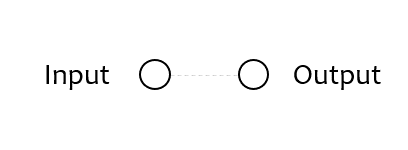
1) Neural Network 구성하기

아래의 예제는 Tensorflow의 가장 간단한 Neural Network를 구현합니다.

import tensorflow as tf
from tensorflow import keras
import numpy as np

model = keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])])

tf.keras (tensorflow.keras)는 TensorFlow의 하이레벨 구현을 위한 Keras API 모듈입니다.

tf.keras 모듈의 Sequential 클래스는 Neural Network의 각 층을 순서대로 쌓을 수 있도록 합니다.

tf.keras.layers 모듈의 Dense 클래스는 (완전 연결된) 하나의 뉴런층을 구현합니다.

units는 뉴런 또는 출력 노드의 개수를 의미하며, 양의 정수로 설정합니다.

input_shape는 입력 데이터의 형태를 결정합니다.

2) Neural Network 컴파일하기

model.compile(loss='mean_squared_error', optimizer='sgd')

다음으로 Neural Network 모델을 컴파일하는 과정에서는,

모델의 학습에 필요한 손실함수 (loss function)와 옵티마이저 (optimizer)를 결정합니다.

손실함수는 Neural Network의 예측이 얼마나 잘 맞는지 측정하는 역할을 하고, 옵티마이저는 더 개선된 예측값을 출력하도록 최적화하는 알고리즘입니다.

예제에서는 각각 mean_squared_error와 SGD (Stochastic Gradient Descent)로 설정했습니다.

경우에 따라 다른 손실함수와 옵티마이저가 더 효과적일 수 있습니다.

더 자세한 내용은 TensorFlow 공식 문서를 참고하세요.

3) Neural Network 훈련하기

Sequantial 클래스의 fit() 메서드는 주어진 입출력 데이터에 대해 지정한 횟수만큼 Neural Network를 훈련합니다.

훈련이 이루어질 때마다, Neural Network는 주어진 입력에 대해 주어진 출력값에 더 가까운 값을 출력하게 됩니다.

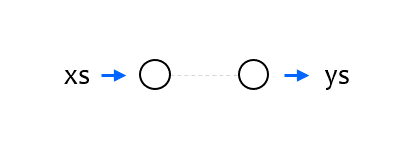
xs = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], dtype=float)
ys = np.array([-3.0, -1.0, 1.0, 3.0, 5.0, 7.0], dtype=float)

model.fit(xs, ys, epochs=500)

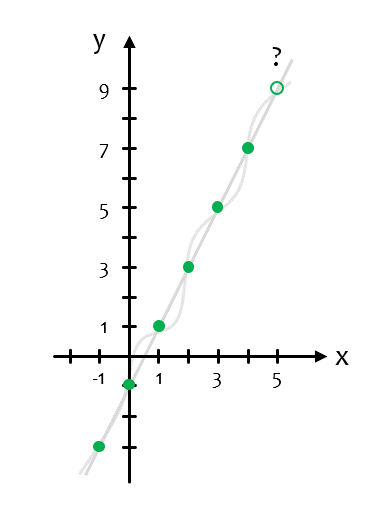
xs, ys는 Neural Network의 훈련에 사용할 입력과 출력 데이터이며, ‘y = 2x - 1’의 관계를 갖는 것처럼 보입니다.

에포크 (epoch)는 주어진 데이터를 한 번 훈련하는 단위입니다.

4) Neural Network 예측하기

Sequantial 클래스의 predict() 메서드를 사용하면 특정 입력에 대해 Neural Network가 출력 (예측)하는 값을 얻을 수 있습니다.

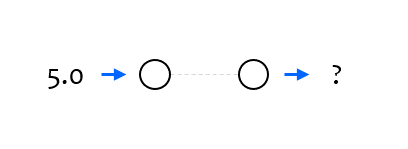
pred = model.predict([5.0])
print(pred)

[[8.993531]]

훈련이 끝난 Neural Network에 숫자 5.0을 입력하면, 약 8.99를 출력합니다.

비록 작은 오차가 있지만, 이제 이 간단한 Neural Network는 어떤 입력 x에 대해서 대략 2x - 1를 출력하도록 훈련되었습니다.

작은 오차가 발생하는 이유는 ‘여섯 개’라는 적은 양의 입출력 데이터를 훈련에 사용했기 때문이고,

또한 모든 x에 대해, 입출력의 관계가 ‘y = 2x - 1’이 아닐 가능성이 있기 때문입니다.

전체 코드

지금까지 작성한 전체 코드와 출력 결과는 아래와 같습니다.

import tensorflow as tf
from tensorflow import keras
import numpy as np

model = keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])])
model.compile(optimizer='sgd', loss='mean_squared_error')

xs = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], dtype=float)
ys = np.array([-3.0, -1.0, 1.0, 3.0, 5.0, 7.0], dtype=float)

model.fit(xs, ys, epochs=500)

pred = model.predict([5.0])
print(pred)

Epoch 1/500
1/1 [==============================] - 0s 1ms/step - loss: 49.7585
Epoch 2/500
1/1 [==============================] - 0s 880us/step - loss: 39.5407
Epoch 3/500
1/1 [==============================] - 0s 981us/step - loss: 31.4938
Epoch 4/500
1/1 [==============================] - 0s 921us/step - loss: 25.1550
Epoch 5/500
1/1 [==============================] - 0s 1ms/step - loss: 20.1601
Epoch 6/500
1/1 [==============================] - 0s 2ms/step - loss: 16.2229
Epoch 7/500
1/1 [==============================] - 0s 1ms/step - loss: 13.1178
Epoch 8/500
1/1 [==============================] - 0s 943us/step - loss: 10.6675
Epoch 9/500
1/1 [==============================] - 0s 3ms/step - loss: 8.7327
Epoch 10/500
1/1 [==============================] - 0s 2ms/step - loss: 7.2035

...

Epoch 200/500
1/1 [==============================] - 0s 3ms/step - loss: 0.0328
Epoch 201/500
1/1 [==============================] - 0s 2ms/step - loss: 0.0321
Epoch 202/500
1/1 [==============================] - 0s 2ms/step - loss: 0.0315
Epoch 203/500
1/1 [==============================] - 0s 1ms/step - loss: 0.0308
Epoch 204/500
1/1 [==============================] - 0s 2ms/step - loss: 0.0302
Epoch 205/500
1/1 [==============================] - 0s 2ms/step - loss: 0.0296
Epoch 206/500
1/1 [==============================] - 0s 2ms/step - loss: 0.0290
Epoch 207/500
1/1 [==============================] - 0s 2ms/step - loss: 0.0284
Epoch 208/500
1/1 [==============================] - 0s 2ms/step - loss: 0.0278
Epoch 209/500
1/1 [==============================] - 0s 2ms/step - loss: 0.0272

...

Epoch 490/500
1/1 [==============================] - 0s 1ms/step - loss: 7.9806e-05
Epoch 491/500
1/1 [==============================] - 0s 5ms/step - loss: 7.8166e-05
Epoch 492/500
1/1 [==============================] - 0s 3ms/step - loss: 7.6561e-05
Epoch 493/500
1/1 [==============================] - 0s 13ms/step - loss: 7.4988e-05
Epoch 494/500
1/1 [==============================] - 0s 3ms/step - loss: 7.3448e-05
Epoch 495/500
1/1 [==============================] - 0s 3ms/step - loss: 7.1940e-05
Epoch 496/500
1/1 [==============================] - 0s 3ms/step - loss: 7.0462e-05
Epoch 497/500
1/1 [==============================] - 0s 2ms/step - loss: 6.9013e-05
Epoch 498/500
1/1 [==============================] - 0s 2ms/step - loss: 6.7596e-05
Epoch 499/500
1/1 [==============================] - 0s 2ms/step - loss: 6.6209e-05
Epoch 500/500
1/1 [==============================] - 0s 3ms/step - loss: 6.4849e-05
[[8.993531]]

이전글/다음글

이전글 : 1. 텐서 기초 살펴보기

다음글 : 3. 손실 함수 살펴보기

공유하기