시계열 데이터 예측하기

Photo by Chris Liverani on Unsplash

이전 페이지에서는 시계열 데이터 (Time Series Data)의 기본적인 특징에 대해 알아보았습니다.

이번에는 시계열 데이터를 예측하는 몇가지 방식에 대해 알아보고, 예측의 오차를 정량화하는 방법을 소개합니다.

시계열 데이터 만들기

예제1

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras

# 1. 기본 스타일 설정
plt.style.use('default')
plt.rcParams['figure.figsize'] = (6, 3)
plt.rcParams['font.size'] = 12


def plot_series(time, series, format="-", start=0, end=None):
    plt.plot(time[start:end], series[start:end], format)
    plt.xlabel("Time")
    plt.ylabel("Value")
    plt.grid(True)

def trend(time, slope=0):
    return slope * time

def seasonal_pattern(season_time):
    return np.where(season_time < 0.4, np.cos(season_time * 2 * np.pi), 1 / np.exp(3 * season_time))

def seasonality(time, period, amplitude=1, phase=0):
    season_time = ((time + phase) % period) / period
    return amplitude * seasonal_pattern(season_time)

def noise(time, noise_level=1, seed=None):
    rnd = np.random.RandomState(seed)
    return rnd.randn(len(time)) * noise_level

time = np.arange(4 * 365 + 1, dtype="float32")
baseline = 10
series = trend(time, 0.1)
baseline = 10
amplitude = 40
slope = 0.05
noise_level = 5

# Create the series
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)

# Update with noise
series += noise(time, noise_level, seed=42)

plot_series(time, series)
plt.show()

이전 페이지에서 소개했던대로 trend(), seasonality(), noise() 함수는 각각 경향성, 계절성, 노이즈를 갖는 시계열 데이터를 반환합니다.

이 함수들을 사용해서 시계열 데이터를 만들고 아래와 같이 시각화했습니다.

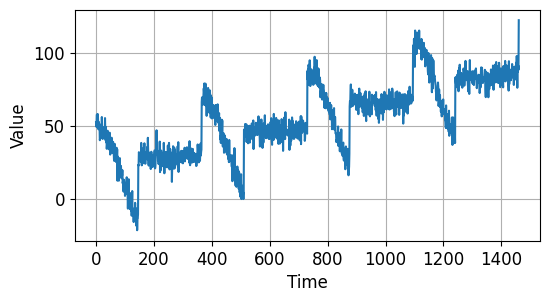
시계열 데이터 예측하기 - 시계열 데이터 만들기

예제2

split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]

time_valid = time[split_time:]
x_valid = series[split_time:]

plot_series(time_train, x_train)
plt.show()

plot_series(time_valid, x_valid)
plt.show()

시계열 데이터의 앞부분 1000개를 훈련용, 그리고 나머지를 검증용 데이터로 분리했습니다.

아래와 같이 두 부분으로 나눠졌습니다.

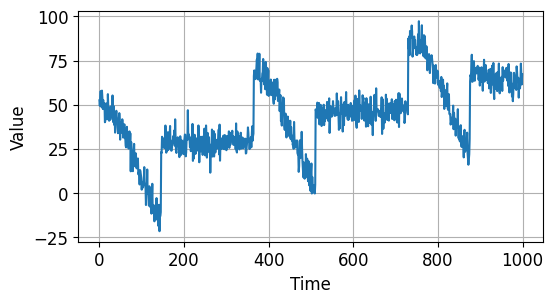
시계열 데이터 예측하기 - 시계열 데이터 만들기 (Train)

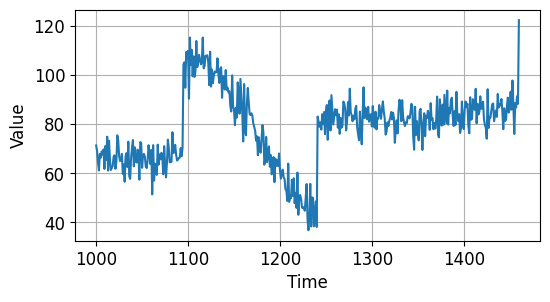
시계열 데이터 예측하기 - 시계열 데이터 만들기 (Validation)

Naive Forecast

예제1

naive_forecast = series[split_time - 1: -1]
plot_series(time_valid, x_valid)
plot_series(time_valid, naive_forecast)

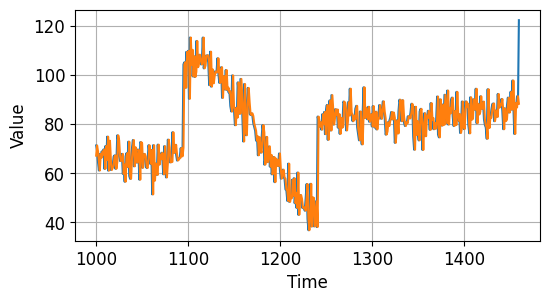
naive_forecast는 말그대로 이전의 데이터를 다음 값으로 예측하는 시계열 데이터입니다.

우선 한 스텝 앞의 데이터를 가져와서 나타내면 아래와 같습니다.

시계열 데이터 예측하기 - Naive Forecast

예제2

plot_series(time_valid, x_valid, start=0, end=150)
plot_series(time_valid, naive_forecast, start=1, end=151)

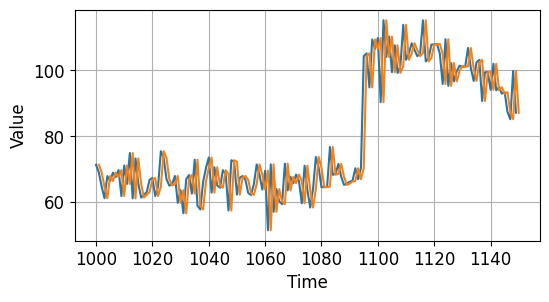
그래프 플롯의 시작 시점을 한 스텝 뒤로 했습니다.

앞에서 150개의 데이터를 나타내면 아래와 같습니다.

시계열 데이터 예측하기 - Naive Forecast

예제3

print(keras.metrics.mean_squared_error(x_valid, naive_forecast).numpy())
print(keras.metrics.mean_absolute_error(x_valid, naive_forecast).numpy())

61.827534
5.937908

keras.metrics 모듈의 mean_squared_error(), mean_absolute_error() 함수는 두 시계열 데이터 간의 오차를 정량화합니다.

각각 61.827534, 5.937908입니다.

지난 30개의 평균값으로 예측하기

예제1

def moving_average_forecast(series, window_size):
    forecast = []
    for time in range(len(series) - window_size):
        forecast.append(series[time: time + window_size].mean())
    return np.array(forecast)

moving_avg = moving_average_forecast(series, 30)[split_time - 30:]

plot_series(time_valid, x_valid)
plot_series(time_valid, moving_avg)

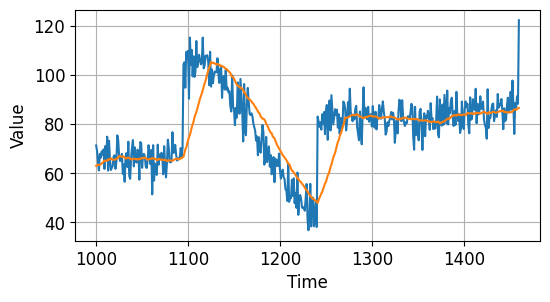
moving_average_forecast() 함수는 window_size 동안의 평균값을 다음 예측값으로 사용합니다.

아래 그림의 주황색 곡선으로 나타냈습니다.

시계열 데이터 예측하기 - 지난 30개의 평균값으로 예측하기

예제2

print(keras.metrics.mean_squared_error(x_valid, moving_avg).numpy())
print(keras.metrics.mean_absolute_error(x_valid, moving_avg).numpy())

106.674576
7.1424184

mean_squared_error(), mean_absolute_error() 함수로 예측의 오차를 확인해보면 각각 106.674576와 7.1424184입니다.

이전글/다음글

이전글 : 시계열 데이터 기초

다음글 : 날씨 데이터셋

공유하기